题目内容
10.已知,点P(x1,-2)、Q(x2,3)、H(x3,1)在双曲线y=$\frac{k}{x}$(k<0)上,那么x1、x2、x3的大小关系是x3<x2<x1.(用“<”连接)分析 先判断出函数的增减性,再根据其坐标特点解答即可.
解答 解:∵k<0,∴反比例函数图象的两个分支在第二四象限,且在每个象限内y随x的增大而增大,
又∵Q(x2,3)、H(x3,1)是双曲线上第二象限的两点,且3>1,
∴x2<x3<0,
又∵P(x1,-2)在第四象限,∴x1>0,故x3<x2<x1.
故答案为x3<x2<x1.
点评 本题考查利用反比例函数的增减性质判断图象上点的坐标特征.

练习册系列答案
相关题目
20.-$\frac{1}{2}$的绝对值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
18.已知等腰三角形的周长为20cm,底边长为ycm,腰长为xcm,则y与x之间的函数关系式为( )
| A. | y=20-2x(0<x<10) | B. | y=10-x(0<x<10) | C. | y=20-2x(5<x<10) | D. | y=10-x(5<x<10) |
5.学校建围栏,要为24000根栏杆油漆,由于改进了技术,每天比原计划多油400根,结果提前两天完成了任务,请问原计划每天油多少根栏杆?如果设原计划每天油x根栏杆,根据题意列方程为( )
| A. | $\frac{24000}{x}$=$\frac{24000}{x-400}$+2 | B. | $\frac{24000}{x}$=$\frac{24000}{x-400}$-2 | ||
| C. | $\frac{24000}{x}$=$\frac{24000}{x+400}$-2 | D. | $\frac{24000}{x}$=$\frac{24000}{x+400}$+2 |
19.对于多项式①x2-y2,②-x2-y2,③4x2-y,④x2-4,能够用平方差公式进行因式分解的是( )
| A. | ①和② | B. | ①和③ | C. | ①和④ | D. | ②和④ |
20.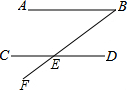 如图所示,AB∥CD,∠DEF=120°,则∠B的度数为( )
如图所示,AB∥CD,∠DEF=120°,则∠B的度数为( )
 如图所示,AB∥CD,∠DEF=120°,则∠B的度数为( )
如图所示,AB∥CD,∠DEF=120°,则∠B的度数为( )| A. | 120° | B. | 60° | C. | 150° | D. | 30° |
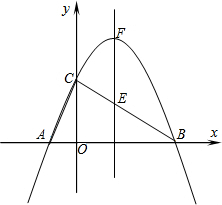 直线y=-$\frac{1}{2}$x+2与坐标轴相交于B、C两点,抛物线也过B、C两点,还与x轴相交于A点,抛物线对称轴与BC相交于E点,顶点为F,∠FEC=∠CAO.
直线y=-$\frac{1}{2}$x+2与坐标轴相交于B、C两点,抛物线也过B、C两点,还与x轴相交于A点,抛物线对称轴与BC相交于E点,顶点为F,∠FEC=∠CAO.