题目内容
如图所示，△ABC中，AB=BD=DC，∠C=40°，则∠A=________，∠ABD=________．
80° 20°
分析：根据等边对等角可得到∠C=∠DBC，∠A=∠ADB，已知∠C=40°，从而利用三角形外角的性质可求得∠ADB的度数，再根据三角形内角和定理即可求得∠ABD的度数．
解答：∵△ABC中，AB=BD=DC，∠C=40°，
∴∠C=∠DBC，∠A=∠ADB，
∵∠C=40°，
∴∠C=∠DBC=40°，∠A=∠ADB=80°，
∴∠ABD=180°-80°-80°=20°．
故答案为：80°，20°．
点评：此题主要考查三角形的内角和定理及三角形的外角性质的综合运用．
分析：根据等边对等角可得到∠C=∠DBC，∠A=∠ADB，已知∠C=40°，从而利用三角形外角的性质可求得∠ADB的度数，再根据三角形内角和定理即可求得∠ABD的度数．
解答：∵△ABC中，AB=BD=DC，∠C=40°，
∴∠C=∠DBC，∠A=∠ADB，
∵∠C=40°，
∴∠C=∠DBC=40°，∠A=∠ADB=80°，
∴∠ABD=180°-80°-80°=20°．
故答案为：80°，20°．
点评：此题主要考查三角形的内角和定理及三角形的外角性质的综合运用．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
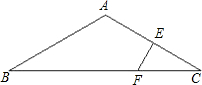如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
16、如图所示，△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、AC于D、E，∠CAE：∠EAB=5：2，则∠B=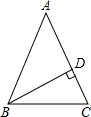
如图所示，△ABC中，AB=AC=10，BD是AC边的高线，DC=2，试求BD的长．
如图所示，△ABC中，BC的垂直平分线交AB于点E，若△ABC的周长为10，BC=4，则△ACE的周长是
如图所示，△ABC中，AB=AC，BD⊥AC，垂足为D，求∠DBC与∠A的关系．