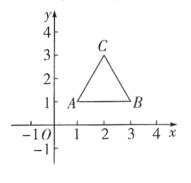Question

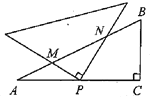
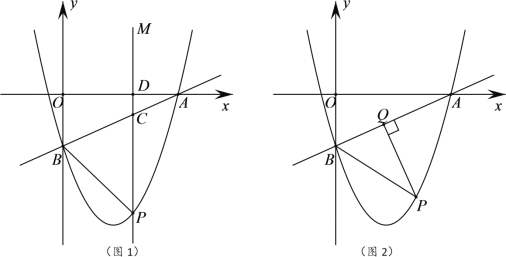
【题目】（1）问题发现

如图1，和均为等边三角形，直线和直线交于点．

填空：①的度数是 ；

②线段，之间的数量关系为 ．

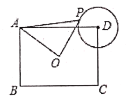
（2）类比探究

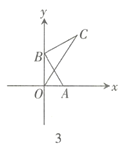
如图2，和均为等腰直角三角形，，，，直线和直线交于点．请判断的度数及线段，之间的数量关系，并说明理由．

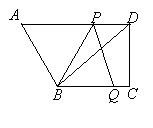
（3）解决问题

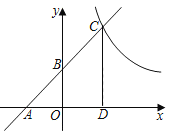
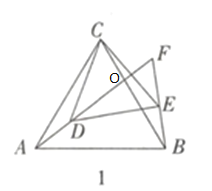
如图3，在平面直角坐标系中，点坐标为，点为轴上任意一点，连接，将绕点逆时针旋转至，连接，请直接写出的最小值．

Answer 1

【答案】（1）①；②

（2）；，理由见解析

（3）的最小值为

【解析】

（1）先证明，可得，即可求得度数，.

（2）先证明，可得，由此即可解决问题；

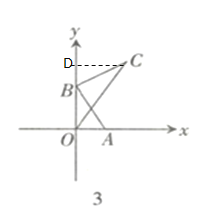
（3）过点C作轴于点D，先证明，可得出，设B(0，a)，则点C（a，4+a），利用勾股定理列出关于a的式子，配方求出OC的最小值即可.

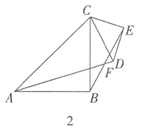
(1)如图1中，

∵△ABC和△CDE均为等边三角形，

∴CA=CB，CD=CE，∠ACB=∠DCE=

∴∠ACD=∠BCE

∴△ACD≌△BCE(SAS)

∴AD=BE，∠CAD=∠CBF

设BC交AF于点O

∵∠AOC=∠BOF

∴∠BFO=∠ACO=60°，

∴∠AFB=；

（2），均为等腰直角三角形

∴

∴△ACD∽△BCE

∴

∵∠AFB+∠CBF=∠ACB+∠CAF

∴∠AFB=∠ACB=；

（3）过点C作轴于点D

∴

∵绕点逆时针旋转得到

∴

∴

∵

∴

∴

∴

设B(0，a)，则点C（a，4+a）

∴

∴当a=-2时，取最小值8，此时OC=，

即OC可取的最小值为.