��Ŀ����
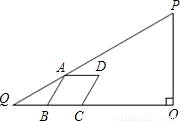
��ͼ����Rt��OPQ�У���POQ=90�㣬��Q=30�㣬OP=4| 3 |
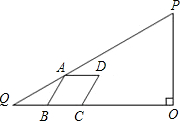 PQ�ϣ�B��C�ڱ�QO�ϣ�B����C�����ࣩ���ҡ�ABC=60�㣮��BQ=x��
PQ�ϣ�B��C�ڱ�QO�ϣ�B����C�����ࣩ���ҡ�ABC=60�㣮��BQ=x����1�����ú�x�Ĵ���ʽ��ʾ����ABCD�ı߳���
��2������D���߶�OP��ʱ����x��ֵ��
��3��������ABCD���OPQ�غϲ��ֵ����Ϊy����y����x�ĺ�����ϵʽ��
��4������PD��OD�����ڲ�ͬ��xֵ������Ƚ��߶�OD��PD�Ĵ�С��ϵ��ֱ��д�����ۣ�
��������1���ã���Q=30�㣬��ABC=60�㣬����������Ƕ����ɵá�QAB=��Q=30�㣬�����ɵ�BA=BQ�����ɵô𰸣�
��2���������⣬�ɵ�Rt��DCO�У��С�DCO=60�㣬CD=x���������ε����ʣ��ɵ�QO=QB+BC+CO���������ݿɵô𰸣�
��3����A��AH��BC��H����Rt��ABH�У���ABH=60�㣬AB=x����0��x��
ʱ��y=x��
x=
x2�������������ݷ����ɵô𰸣�
��4����OP���д��ߣ���ϴ�ֱƽ���ߵ����ʣ��ɵô𰸣�
��2���������⣬�ɵ�Rt��DCO�У��С�DCO=60�㣬CD=x���������ε����ʣ��ɵ�QO=QB+BC+CO���������ݿɵô𰸣�
��3����A��AH��BC��H����Rt��ABH�У���ABH=60�㣬AB=x����0��x��
| 24 |
| 5 |
| ||
| 2 |
| ||
| 2 |
��4����OP���д��ߣ���ϴ�ֱƽ���ߵ����ʣ��ɵô𰸣�
��� �⣺��1���ߡ�Q=30�㣬��ABC=60�㣬���QAB=��Q=30�㣮
�⣺��1���ߡ�Q=30�㣬��ABC=60�㣬���QAB=��Q=30�㣮
��BA=BQ=x�������εı߳�Ϊx����2�֣�
��2����ͼ�٣���Rt��DCO�У�
�ߡ�DCO=60�㣬CD=x��
��CO=
x��
��QO=QB+BC+CO=x+x+
x
��Rt��POQ�У���Q=30�㣬PO=4
��
��QO=12����
x=12
x=
����2�֣�
��3����ͼ�٣���A��AH��BC��H��
��Rt��ABH�У���ABH=60�㣬AB=x����AH=
x
�൱0��x��
ʱ��
y=x��
x=
x2��2�֣�
��ͼ�ڣ���CD��0P��ؽ��ڵ�E��AD��OP�ཻ�ڵ�F��
��Rt��COE�У���ECO=60�㣬CO=12-2x��
��CE=24-4x����CD=x����DE=5x-24��
��Rt��DFE�У���D=60�㣬
��DF=
-12��EF=
(
-12)?
?��
��x��6ʱ?��
 y=
y=
x2-
��
-12��2=-
x2+30
x-72
��
��4����ͼ�ۣ���OP���д���
��0��x��4ʱ��OD��DP��
��x=4ʱ��OD=DP��
��4��x��6ʱ��OD��DP��
 �⣺��1���ߡ�Q=30�㣬��ABC=60�㣬���QAB=��Q=30�㣮
�⣺��1���ߡ�Q=30�㣬��ABC=60�㣬���QAB=��Q=30�㣮��BA=BQ=x�������εı߳�Ϊx����2�֣�
��2����ͼ�٣���Rt��DCO�У�
�ߡ�DCO=60�㣬CD=x��
��CO=
| 1 |
| 2 |
��QO=QB+BC+CO=x+x+
| 1 |
| 2 |
��Rt��POQ�У���Q=30�㣬PO=4
| 3 |
��QO=12����
| 5 |
| 2 |
x=
| 24 |
| 5 |
��3����ͼ�٣���A��AH��BC��H��
��Rt��ABH�У���ABH=60�㣬AB=x����AH=
| ||
| 2 |
�൱0��x��
| 24 |
| 5 |
y=x��
| ||
| 2 |
| ||
| 2 |

��ͼ�ڣ���CD��0P��ؽ��ڵ�E��AD��OP�ཻ�ڵ�F��
��Rt��COE�У���ECO=60�㣬CO=12-2x��
��CE=24-4x����CD=x����DE=5x-24��
��Rt��DFE�У���D=60�㣬
��DF=
| 5x |
| 2 |
| 3 |
| 5x |
| 2 |
?��
| 24 |
| 5 |
 y=
y=
| ||
| 2 |
| ||
| 2 |
| 5x |
| 2 |
21
| ||
| 8 |
| 3 |
| 3 |
��4����ͼ�ۣ���OP���д���
��0��x��4ʱ��OD��DP��
��x=4ʱ��OD=DP��
��4��x��6ʱ��OD��DP��
���������⿼�����ε����ʣ�ע��������ε����ʣ��õ������Ĺ�ϵ����������������⣮

��ϰ��ϵ�д�
�����Ŀ
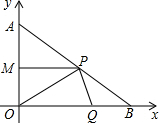 �ֱ�ΪAB��OB���ϵĶ�������ͬʱ�ֱ�ӵ�A��O��B�������˶����ٶȾ�Ϊ1cm/�룬��P��Q�ƶ�ʱ��Ϊt��0��t��4��
�ֱ�ΪAB��OB���ϵĶ�������ͬʱ�ֱ�ӵ�A��O��B�������˶����ٶȾ�Ϊ1cm/�룬��P��Q�ƶ�ʱ��Ϊt��0��t��4�� ���ı���ABCD�����Σ���A�ڱ�
���ı���ABCD�����Σ���A�ڱ�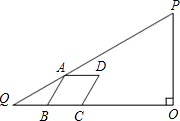 PQ�ϣ�B��C�ڱ�QO�ϣ�B����C�����ࣩ���ҡ�ABC=60�㣮��BQ=x��
PQ�ϣ�B��C�ڱ�QO�ϣ�B����C�����ࣩ���ҡ�ABC=60�㣮��BQ=x��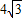 ���ı���ABCD�����Σ���A�ڱ�PQ�ϣ�B��C�ڱ�QO�ϣ�B����C�����ࣩ���ҡ�ABC=60°����BQ=x��
���ı���ABCD�����Σ���A�ڱ�PQ�ϣ�B��C�ڱ�QO�ϣ�B����C�����ࣩ���ҡ�ABC=60°����BQ=x��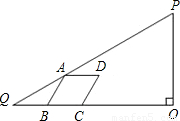
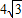 ���ı���ABCD�����Σ���A�ڱ�PQ�ϣ�B��C�ڱ�QO�ϣ�B����C�����ࣩ���ҡ�ABC=60°����BQ=x��
���ı���ABCD�����Σ���A�ڱ�PQ�ϣ�B��C�ڱ�QO�ϣ�B����C�����ࣩ���ҡ�ABC=60°����BQ=x��