Question

【题目】如图，∠ACB＝120°，以AC、BC为边向外作等边△ACF和等边△BCF，点P、M、N分别为AB、CF、CE的中点

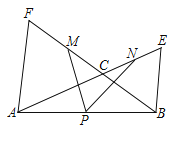
(1) 求证：PM＝PN

(2) 求证：

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）取AC中点G，BC中点H，连接MG、PG、PH、HN，根据三角形中位线定理找到条件，证明△MGP≌△PHN即可；

（2）由（1）可知CM=CG=AG，PG=CH=CN，然后求出∠MCN=∠AGP =120°，证明△AGP≌△MCN即可．

证明：（1）取AC中点G，BC中点H，连接MG、PG、PH、HN．

∵△ACF、△BCE都是等边三角形，

∴AC＝AF＝CF，∠CAF＝∠ACF＝60°，BC＝CE＝BE，∠CBE＝∠BCE＝60°，

∵CM＝MF，CG＝AG，

∴GM∥AF，GM＝AF，同理PH＝AC，PH∥AC，PG＝BC，PG∥BC，HN＝BE，HN∥BE，

∴GM＝PH，PG＝HN，

∴∠CGM＝∠CAF＝60°，∠CHN＝∠CBE＝60°，四边形CHPG是平行四边形，

∴∠CGP＝∠CHP，∠CGM＝∠CHN，

∴∠MGP＝∠PHN，

在△MGP和△PHN中， ，

∴△MGP≌△PHN，

∴PM＝PN．

（2）由（1）可知CM=CG=AG，PG=CH=CN，

∠MCN=360°-∠FCA-∠ACB-∠BCE=360°-60°-120°-60°=120°，∠AGP=∠ACB=120°，

在△AGP和△MCN中，，

∴△AGP≌△MCN，

∴AP=MN，

∵，

∴.