题目内容
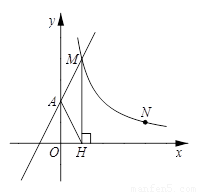
如图,直线 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线 在第一象限交于B、C两点,且AB•AC=4,则k= .
在第一象限交于B、C两点,且AB•AC=4,则k= .
【答案】分析:先求出直线与x轴和y轴的两交点D与A的坐标,根据OA与OD的长度求出比值即可得到角ADO的正切值,利用特殊角的三角函数值即可求出角ADO的度数,然后过B和C分别作y轴的垂线,分别交于E和F点,联立直线与双曲线方程,消去y后得到关于x的一元二次方程,利用韦达定理即可表示出EB与FC的积,然后在直角三角形AEB中利用cos∠ABE表示出EB与AB的关系,同理在直角三角形AFC中,利用cos∠ACF表示出FC与AC的关系,根据AB•AC=4列出关于k的方程,求出方程的解即可得到k的值.
解答: 解:对直线方程
解:对直线方程 ,令y=0,得到x=
,令y=0,得到x= b,即直线与x轴的交点D的坐标为(
b,即直线与x轴的交点D的坐标为( b,0),
b,0),
令x=0,得到y=b,即A点坐标为(0,b),
∴OA=b,OD= b,
b,
∵在Rt△AOD中,tan∠ADO= =
= ,
,
∴∠ADO=30°,即直线y=- +b与x轴的夹角为30°,
+b与x轴的夹角为30°,
∵直线y=- x+b与双曲线y=
x+b与双曲线y= 在第一象限交于点B、C两点,
在第一象限交于点B、C两点,
∴- x+b=
x+b= ,即-
,即- x2+bx-k=0,
x2+bx-k=0,
由韦达定理得:x1x2= =
= k,即EB•FC=
k,即EB•FC= k,
k,
∵ =cos30°=
=cos30°= ,
,
∴AB= EB,
EB,
同理可得:AC= FC,
FC,
∴AB•AC=( EB)(
EB)( FC)=
FC)= EB•FC=
EB•FC=
 k=4,
k=4,
解得:k= .
.
点评:本题考查函数图象交点坐标的求法,同时考查了三角函数的知识,难度较大.
解答:
 解:对直线方程
解:对直线方程 ,令y=0,得到x=
,令y=0,得到x= b,即直线与x轴的交点D的坐标为(
b,即直线与x轴的交点D的坐标为( b,0),
b,0),令x=0,得到y=b,即A点坐标为(0,b),
∴OA=b,OD=
 b,
b,∵在Rt△AOD中,tan∠ADO=
 =
= ,
,∴∠ADO=30°,即直线y=-
 +b与x轴的夹角为30°,
+b与x轴的夹角为30°,∵直线y=-
 x+b与双曲线y=
x+b与双曲线y= 在第一象限交于点B、C两点,
在第一象限交于点B、C两点,∴-
 x+b=
x+b= ,即-
,即- x2+bx-k=0,
x2+bx-k=0,由韦达定理得:x1x2=
 =
= k,即EB•FC=
k,即EB•FC= k,
k,∵
 =cos30°=
=cos30°= ,
,∴AB=
 EB,
EB,同理可得:AC=
 FC,
FC,∴AB•AC=(
 EB)(
EB)( FC)=
FC)= EB•FC=
EB•FC=
 k=4,
k=4,解得:k=
 .
.点评:本题考查函数图象交点坐标的求法,同时考查了三角函数的知识,难度较大.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
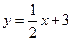 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.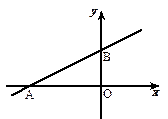
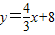 与x轴交于A点,与y轴交于B点,M是△ABO的内心,函数
与x轴交于A点,与y轴交于B点,M是△ABO的内心,函数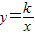 的图象经过M点,则k= .
的图象经过M点,则k= .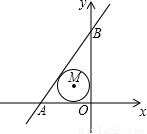
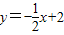 与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=
与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=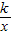 (k<0)经过点B,则k的值为( )
(k<0)经过点B,则k的值为( )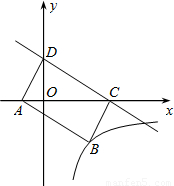
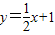 与y轴交于A点,过点A的抛物线
与y轴交于A点,过点A的抛物线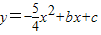 与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).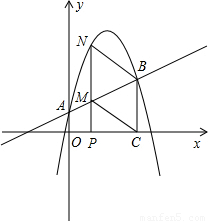
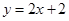 与y轴交于A点,与反比例函数
与y轴交于A点,与反比例函数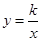 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.