题目内容
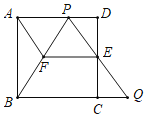
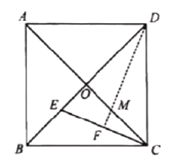
【题目】如图,边长为![]() 的正方形
的正方形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,将正方形
,将正方形![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() ,则
,则![]()
![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
过点M作MP⊥CD垂足为P,过点O作OQ⊥CD垂足为Q,根据正方形的性质得到AB=AD=BC=CD=![]() ,∠DCB=∠COD=∠BOC=90°,根据折叠的性质得到∠EDF=∠CDF,设OM=PM=x,根据相似三角形的性质即可得到结论.
,∠DCB=∠COD=∠BOC=90°,根据折叠的性质得到∠EDF=∠CDF,设OM=PM=x,根据相似三角形的性质即可得到结论.
过点M作MP⊥CD垂足为P,过点O作OQ⊥CD垂足为Q,

∵ 正方形的边长为![]() ,
,
∴OD=1, OC=1, OQ=DQ=![]() ,由折叠可知,∠EDF=∠CDF.
,由折叠可知,∠EDF=∠CDF.
又∵AC⊥BD, ∴OM=PM,
设OM=PM=x
∵OQ⊥CD,MP⊥CD
∴∠OQC=∠MPC=900, ∠PCM=∠QCO,
∴△CMP∽△COQ
∴![]() , 即
, 即 , 解得x=
, 解得x=![]() -1
-1
∴OM=PM=![]() -1.
-1.
故选D

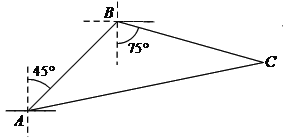
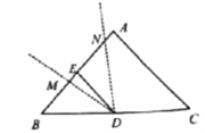
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() ,角的两边分别交直线
,角的两边分别交直线![]() 于
于![]() 两点,设
两点,设![]() 点间的距离为
点间的距离为![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是根据![]() 两点间的距离
两点间的距离![]() 进行取点、画图、测量,分别得到了 与 的几组对应值:
进行取点、画图、测量,分别得到了 与 的几组对应值:
| 0 | 0.30 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| 3.00 | 3.50 | 3.68 | 3.81 | 3.90 | 3.93 | 4.10 |
| 2.88 | 2.81 | 2.69 | 2.67 | 2.80 | 3.15 | 3.85 | 5.24 | 6.01 | 6.71 | 7.27 | 7.44 | 8.87 |
请你通过计算,补全表格
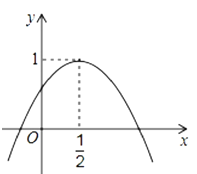
(2)描点、连线:在平面直角坐标系![]() 中,描出表中各组数值所对应的点
中,描出表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象:
的图象:

(3)探究性质:随着自变量![]() 的不断增大,函数
的不断增大,函数![]() 的变化趋势:
的变化趋势:
(4)解决问题:当![]() 时,
时,![]() 的长度大约是____
的长度大约是____![]() (保留两位小数).
(保留两位小数).