题目内容
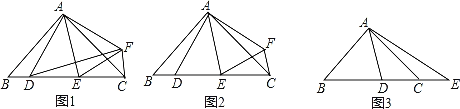
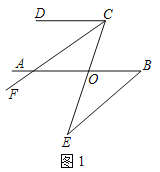
【题目】（1）如图1，AB∥CD，CF平分∠DCE，若∠DCF＝30°，∠E＝20°，求∠ABE的度数．
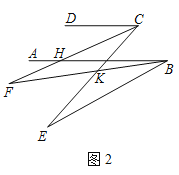
（2）如图2，已知AB∥CD，CF平分∠DCE，∠EBF＝2∠ABF，若∠F的2倍与∠E的补角的和为190°，求∠ABE的度数．
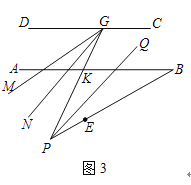
（3）如图3，若P是（2）中的射线BE上一点，G是CD上任一点，PQ∥GN，PQ平分∠BPG，GM平分∠DGP，若∠B＝30°，求∠MGN的度数．
【答案】（1）∠ABE＝40°；（2）∠ABE＝30°；（3）∠MGN＝15°
【解析】
（1）过E作EM∥AB，根据平行线的判定与性质和角平分线的定义解答即可；
（2）过E作EM∥AB，过F作FN∥AB，根据平行线的判定与性质，角平分线的定义以及解一元一次方程解答即可；
（3）过P作PL∥AB，根据平行线的判定与性质，三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义解答即可．
解：（1）过E作EM∥AB，
∵AB∥CD，
∴CD∥EM∥AB，
∴∠ABE＝∠BEM，
∠DCE＝∠CEM，
∵CF平分∠DCE，
∴∠DCE＝2∠DCF，
∵∠DCF＝30°，
∴∠DCE＝60°，
∴∠CEM＝60°，
又∵∠CEB＝20°，
∴∠BEM＝∠CEM﹣∠CEB＝40°，
∴∠ABE＝40°；
（2）过E作EM∥AB，过F作FN∥AB，
∵∠EBF＝2∠ABF，
∴设∠ABF＝x，∠EBF＝2x，则∠ABE＝3x，
∵CF平分∠DCE，
∴设∠DCF＝∠ECF＝y，则∠DCE＝2y，
∵AB∥CD，
∴EM∥AB∥CD，
∴∠DCE＝∠CEM＝2y，
∠BEM＝∠ABE＝3x，
∴∠CEB＝∠CEM﹣∠BEM＝2y﹣3x，
同理∠CFB＝y﹣x，
∵2∠CFB+（180°﹣∠CEB）＝190°，
∴2（y﹣x）+180°﹣（2y﹣3x）＝190°，
∴x＝10°，
∴∠ABE＝3x＝30°；
（3）过P作PL∥AB，
∵GM平分∠DGP，
∴设∠DGM＝∠PGM＝y，则∠DGP＝2y，
∵PQ平分∠BPG，
∴设∠BPQ＝∠GPQ＝x，则∠BPG＝2x，
∵PQ∥QN，
∴∠PGN＝∠GPQ＝x，
∵AB∥CD，
∴PL∥AB∥CD，
∴∠GPL＝∠DGP＝2y，
∠BPL＝∠ABP＝30°，
∵∠BPL＝∠GPL﹣∠BPG，
∴30°＝2y﹣2x，
∴y﹣x＝15°，
∵∠MGN＝∠PGM﹣∠PGN＝y﹣x，
∴∠MGN＝15°．
