Question

【题目】如图，在△ABC中，AD为∠BAC的平分线，BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为（ ）

A.∠ABC=2∠CB.∠ABC=∠CC.∠ABC=∠CD.∠ABC=3∠C

Answer 1

【答案】D

【解析】

延长BM到E,证明△ABF≌△AEM,利用线段长度推出△BCE是等腰三角形,再根据角度转换求出即可.

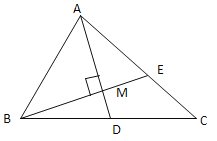
证明:延长BM，交AC于E，

∵AD平分∠BAC，BM⊥AD，

∴∠BAM=∠EAM，∠AMB=∠AME

又∵AM=AM，

∴△ABM≌△AEM，

∴BM=ME，AE=AB，∠AEB=∠ABE,

∴BE=BM+ME=4，AE=AB=5,

∴CE=AC-AE=9-5=4,

∴CE=BE，

∴△BCE是等腰三角形，

∴∠EBC=∠C，

又∵∠ABE=∠AEB=∠C+∠EBC.

∴∠ABE=2∠C，

∴∠ABC=∠ABE+∠EBC=3∠C.

故选D.