题目内容
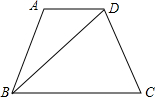
如图,等腰梯形ABCD,周长为40,∠BAD=60°,BD平分∠ABC,则CD的长为：
- A.4
- B.5
- C.8
- D.10
C
本题主要考查了等腰梯形的性质. 根据BD平分∠ABC可判断出△DCB是等腰三角形，再结合∠A=60°可确定△ABD是直角三角形，从而设CD=x，利用周长可求出答案．
解：∵BD平分∠ABC，
∴∠CDB=∠DBA=∠BDC=30°，
∴DC=CB=AD，
又∵∠A=60°，
∴△ABD是直角三角形，
设CD=x，则AD=CD=CB=x，AB=2AD=2x，
∴5x=40，
∴x=8cm．
故选C．
本题主要考查了等腰梯形的性质. 根据BD平分∠ABC可判断出△DCB是等腰三角形，再结合∠A=60°可确定△ABD是直角三角形，从而设CD=x，利用周长可求出答案．
解：∵BD平分∠ABC，
∴∠CDB=∠DBA=∠BDC=30°，
∴DC=CB=AD，
又∵∠A=60°，
∴△ABD是直角三角形，
设CD=x，则AD=CD=CB=x，AB=2AD=2x，
∴5x=40，
∴x=8cm．
故选C．
练习册系列答案
阅读快车系列答案
相关题目
如图等腰梯形ABCD中，AD∥BC，AB=CD，BD平分∠ABC，BD⊥CD．若AD=2cm，则BD=
如图等腰梯形ABCD中，AD∥BC，BD平分∠ABC，∠DBC=30°，AD=5，则BC=
.
S梯形ABCD ?若存在,请求出该点坐标,若不存在,请说明理由.
