题目内容
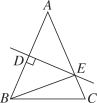
【题目】如图,Rt△ABC中,∠ACB=90°,AC边上的垂直平分线交AC于D,交AB于E,延长DE到F,使BF=CE
(1)四边形BCEF是平行四边形吗?说说你的理由.
(2)当∠A等于多少时,四边形BCEF是菱形,并说出你的理由.
(3)四边形BCEF可以是正方形吗?为什么?
【答案】
(1)解:四边形BCEF是平行四边形,理由如下:
证明:∵DF垂直且平分AC且∠ACB=90°
∴FD∥BC,AE=CE,
∴∠A=∠ACE,
∵∠A+∠ABC=∠ACE+∠BCE=90°,
∴∠ABC=∠BCE,
∴BE=CE=BF,
∴∠BFE=∠BEF
∵FD∥BC,
∴∠BFE=∠BEF=∠ABC=∠BCE
∴∠FBE=∠BEC,
∴FB∥EC,
∵CE=BF,
∴四边形BCEF为平行四边形;
(2)解:∠A=30°,
证明:∵∠A=30°,
∴∠ABC=60°且BE=CE,
∴△BCE为等边三角形,
∴BC=CE,
由(1)可知四边形BCEF为平行四边形,
∴四边形BCEF为菱形;
(3)解:不可以,
因为∠BCE始终是锐角,所以四边形BCEF不可能是正方形.
【解析】(1)根据已知,先证明FD∥BC得出∠BEF=∠ABC,再根据线段垂直平分线的性质推出∠A=∠ACE,根据等教的余角相等得出∠ABC=∠BCE,证得BE=CE=BF,得出∠BFE=∠BEF,然后证明FB∥EC,即可得出结论。
(2)四边形BCEF是平行四边形,要证明它是菱形,只需证明一组邻边相等,已征得BE=CE,若BC=CE,则BE=BC=CE,即得△BCE为等边三角形,因此∠A=30°。
(3)根据题意可知0°<∠BCE<90°,因此四边形BCEF不可能是正方形。
【考点精析】掌握线段垂直平分线的性质和平行四边形的判定是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.