题目内容
【题目】我市东湖高新技术开发区某科技公司,用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价不低于100元,但不超过200元.设销售单价为x(元),年销售量为y(万件),年获利为w(万元)该产品年销售量y(万件)与产品售价x(元)之间的函数关系如图所示.
(1)直接写出y与x之间的函数关系式,并写出x的取值范围;
(2)求第一年的年获利w与x间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?并求当盈利最大或亏损最小时的产品售价;
(3)在(2)的条件下.即在盈利最大或亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利不低于1370万元?若能,求出第二年的售价在什么范围内;若不能,请说明理由.

【答案】(1)y=﹣![]() x+30(100≤x≤200);(2)x=170,w最大值=1690<1520+480=2000,第一年公司亏损,最少亏损是310万元,此时售价为170元;(3)当两年共盈利不低于1370万元时,160≤x≤180.
x+30(100≤x≤200);(2)x=170,w最大值=1690<1520+480=2000,第一年公司亏损,最少亏损是310万元,此时售价为170元;(3)当两年共盈利不低于1370万元时,160≤x≤180.
【解析】
(1)利用待定系数法求解可得;
(2)根据“年获利=(售价-成本价)×销售量”列出函数解析式,配方成顶点式得出其获利最大值,与前期总投入480+1520比较可得;
(3)根据“年获利=1370+前期最少亏损钱数”求得x的值,从而得出答案.
解:(1)设y=kx+b,
将(100,20)和(200,10)代入,得:![]() ,
,
解得: ,
,
∴y=﹣![]() x+30(100≤x≤200);
x+30(100≤x≤200);
(2)w=(﹣![]() x+30)(x﹣40)
x+30)(x﹣40)
=﹣![]() x2+34x﹣1200
x2+34x﹣1200
=﹣![]() (x﹣170)2+1690,
(x﹣170)2+1690,
∵﹣![]() <0,
<0,
∴x=170,w最大值=1690<1520+480=2000,第一年公司亏损,最少亏损是310万元,此时售价为170元;
(3)当﹣![]() x2+34x﹣1200=1370+310=1680时,
x2+34x﹣1200=1370+310=1680时,
解得:x1=160,x2=180,
结合图象当两年共盈利不低于1370万元时,160≤x≤180.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
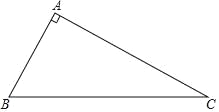
同步学典一课多练系列答案【题目】如图,将△ABC绕顶点C逆时针旋转得到△A′B′C′,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( )
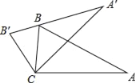
A. 30° B. 35° C. 40° D. 45°
【题目】已知二次函数y=ax2+bx+c,如表给出了y与x的部分对应值:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | n | 3 | 0 | ﹣5 | ﹣12 | … |
(1)根据表格中的数据,试确定二次函数的解析式和n的值;
(2)抛物线y=ax2+bx+c与直线y=2x+m没有交点,求m的取值范围.