题目内容
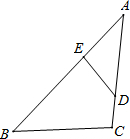如图，要判定△ABC与△AED相似，欲添加一个条件，下列可行的条件有（ ）①AE：BE=AD：DC；②AE：AD=AC：AB；③AD：AC=DE：BC；④∠BED+∠C=180°；⑤∠BED=∠C．
分析：由∠A=∠A，得出要判定△ABC与△AED相似，根据有两边对应成比例，且夹角相等的两三角形相似得出只要具备条件
=
或
=
即可；或根据有两角对应相等的两三角形相似，判断即可．
| AE |
| AB |
| AD |
| AC |
| AE |
| AC |
| AD |
| AB |
解答：解：∵∠A=∠A，
∴要判定△ABC与△AED相似，根据有两边对应成比例，且夹角相等的两三角形相似得出只要具备条件
=
或
=
即可；
∵
=
，
∴
=
，
∴
+1=
+1，
∴
=
，
∴
=
，∴①正确；
∵
=
，
∴
=
，∴②正确；
∵
=
，∴③错误；
∵∠BED+∠C=180°，
∴∠B+∠EDC=360°-180°=180°，
∵∠ADE+∠EDC=180°，
∴∠B=∠ADE，
∵∠A=∠A，
∴△AED∽△ACB，∴④正确；
∵∠A=∠A，∠BED=∠C不能推出两三角形相似，∴⑤错误；
即正确的有①②④，共3个，
故选C．
∴要判定△ABC与△AED相似，根据有两边对应成比例，且夹角相等的两三角形相似得出只要具备条件
| AE |
| AB |
| AD |
| AC |
| AE |
| AC |
| AD |
| AB |
∵
| AE |
| BE |
| AD |
| DC |
∴
| BE |
| AE |
| CD |
| AD |
∴
| BE |
| AE |
| CD |
| AD |
∴
| AB |
| AE |
| AC |
| AD |
∴
| AE |
| AB |
| AD |
| AC |
∵
| AE |
| AD |
| AC |
| AB |
∴
| AE |
| AC |
| AD |
| AB |
∵
| AD |
| AC |
| DE |
| BC |
∵∠BED+∠C=180°，
∴∠B+∠EDC=360°-180°=180°，
∵∠ADE+∠EDC=180°，
∴∠B=∠ADE，
∵∠A=∠A，
∴△AED∽△ACB，∴④正确；
∵∠A=∠A，∠BED=∠C不能推出两三角形相似，∴⑤错误；
即正确的有①②④，共3个，
故选C．
点评：本题考查了相似三角形的判定定理的应用，注意：①有两边对应成比例，且夹角相等的两三角形相似，②有两角对应相等的两三角形相似．
练习册系列答案
相关题目
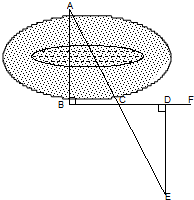19、如图，要测量池塘两岸相对A、B两点的距离，可以在AB的垂线BF上取两点C、D，使BC=CD，再画出BF的垂线DE，使E与A、C在一条直线上，这时测得DE的长就是AB的长，其中可根据
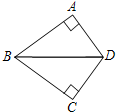如图，∠A=∠C=90°，要判定△ABC≌△CBD，所要添加的一个条件是
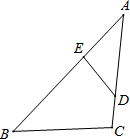如图，要判定△ABC与△AED相似，欲添加一个条件，下列可行的条件有