题目内容
已知CE与⊙O相切于点C,点A在⊙O上,AE⊥CE于E,OE交⊙O于点F
(1)如图(1),若EF=1,CE=3,求sin∠OEA的值;
(2)若tan∠ECF=
,求sin∠OEA的值.
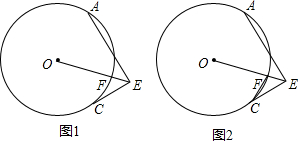
(1)如图(1),若EF=1,CE=3,求sin∠OEA的值;
(2)若tan∠ECF=
| 1 |
| 2 |

考点:切线的性质
专题:
分析:(1)连接OC,在Rt△OCE中可求得OC,又OC∥AE,可求得∠OEA=∠EOC,在Rt△OCE中可求得sin∠EOC,则可得出答案;
(2)连接OC,延长EO交⊙O于点M,连接CM,则可证明△CEF∽△MEC,可求得ME=2CE=4EF,可求得CE:OE,同(1)可求得答案.
(2)连接OC,延长EO交⊙O于点M,连接CM,则可证明△CEF∽△MEC,可求得ME=2CE=4EF,可求得CE:OE,同(1)可求得答案.
解答:解:(1)如图1,连接OC,

∵CE是⊙O的切线,
∴OC⊥CE,
又∵AE⊥CE,
∴OC∥AE,
∴∠OEA=∠EOC,
在Rt△OCE中,由勾股定理可得OC2+CE2=OE2,
即OC2+32=(OF+EF)2=(0C+1)2,解得OC=4,
∴OE=4+1=5,
在Rt△OEC中,sin∠EOC=
=
,
∴sin∠OEA=
;
(2)如图2,连接OC,延长EO交⊙O于点M,连接CM,

∵CE是⊙O的切线,MF为⊙O的直径,
∴OC⊥CE,MC⊥CF,
∴∠MCO+∠OCF=∠OCF+∠FCE,
∴∠MCO=∠FCE,
又∵OM=OC,
∴∠M=∠MCO,
∴∠M=∠FCE,且∠E=∠E,
∴△CEF∽△MEC,
又∵tan∠ECF=
,
∴
=
=
=
,
∴ME=2CE=4EF,
∴MF=3EF,则OF=
EF,
∴OE=
EF,
∴sin∠EOC=
=
=
,
同(1)可得sin∠OEA=sin∠EOC=
.

∵CE是⊙O的切线,
∴OC⊥CE,
又∵AE⊥CE,
∴OC∥AE,
∴∠OEA=∠EOC,
在Rt△OCE中,由勾股定理可得OC2+CE2=OE2,
即OC2+32=(OF+EF)2=(0C+1)2,解得OC=4,
∴OE=4+1=5,
在Rt△OEC中,sin∠EOC=
| CE |
| OE |
| 3 |
| 5 |
∴sin∠OEA=
| 3 |
| 5 |
(2)如图2,连接OC,延长EO交⊙O于点M,连接CM,

∵CE是⊙O的切线,MF为⊙O的直径,
∴OC⊥CE,MC⊥CF,
∴∠MCO+∠OCF=∠OCF+∠FCE,
∴∠MCO=∠FCE,
又∵OM=OC,
∴∠M=∠MCO,
∴∠M=∠FCE,且∠E=∠E,
∴△CEF∽△MEC,
又∵tan∠ECF=
| 1 |
| 2 |
∴
| CF |
| CM |
| CE |
| ME |
| EF |
| CE |
| 1 |
| 2 |
∴ME=2CE=4EF,
∴MF=3EF,则OF=
| 3 |
| 2 |
∴OE=
| 5 |
| 2 |
∴sin∠EOC=
| CE |
| OE |
| 2EF | ||
|
| 4 |
| 5 |
同(1)可得sin∠OEA=sin∠EOC=
| 4 |
| 5 |
点评:本题主要考查切线的性质和相似三角形的判定和性质,在(1)中证得角相等是解题的关键,在(2)中利用正切值,求得线段的比得到OE和CE的关系是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
若式子
有意义,则x的取值范围为( )
| 1 | ||
4-
|
| A、x≥0 |
| B、x≠16 |
| C、x>0且x≠16 |
| D、x≥0且x≠16 |
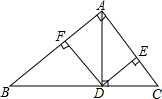 如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )
如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( ) 如图,正三角形ABC的边长为2,点A,B在半径为
如图,正三角形ABC的边长为2,点A,B在半径为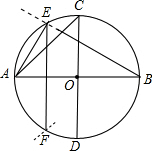 如图,在⊙O中,如果作两条互相垂直的直径AB、CD,那么弦AC是⊙O的内接正方形的一边;如果以点A为圆心,以OA为半径画弧,与⊙O相交于点E,F,那么弦AE、CE、EF分别是⊙O的内接正六边形、正十二边形、正三角形的一边,为什么?
如图,在⊙O中,如果作两条互相垂直的直径AB、CD,那么弦AC是⊙O的内接正方形的一边;如果以点A为圆心,以OA为半径画弧,与⊙O相交于点E,F,那么弦AE、CE、EF分别是⊙O的内接正六边形、正十二边形、正三角形的一边,为什么?