题目内容
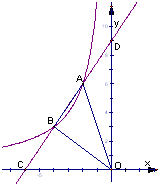
 如图,直线AB与x轴、y轴分别交于点A、B,点A的坐标是(2,0),∠ABO=30°.在坐标平面内,是否存在点P(除点O外),使得△APB与△AOB全等.请写出所有符合条件的点P的坐标________.
如图,直线AB与x轴、y轴分别交于点A、B,点A的坐标是(2,0),∠ABO=30°.在坐标平面内,是否存在点P(除点O外),使得△APB与△AOB全等.请写出所有符合条件的点P的坐标________.
(0,0)或(2,2 )或(-1,
)或(-1, )或(3,
)或(3, )
)
分析:根据题意分为四种情况,画出图形,根据全等三角形性质和含30度角的直角三角形性质,勾股定理求出即可.
解答:∵点A的坐标是(2,0),∠ABO=30°,
∴OA=2,AB=2AO=4,由勾股定理得:OB=2 ,
,
分为四种情况:①当P和O重合时,符合条件,此时P的坐标是(0,0);
②
如图1,此时PB=OA=2,PA=OB=2 ,
,
即P的坐标是(2,2 );
);
③
如图2,过P作PM⊥OA于M,
则∠PAM=60°-30°=30°,
∴PM= AP=
AP= OB=
OB= ,
,
AM= PM=3,
PM=3,
∴OM=3-2=1,
∴P的坐标是(-1, );
);
④
如图3,过P作PM⊥OA于M,
则∠PAM=180°-60°-60°=60°,
∴∠APM=30°,
∴AM= AP=
AP= OA=1,
OA=1,
∴PM= AM=
AM= ,OM=1+2=3,
,OM=1+2=3,
∴P的坐标是(3, ),
),
故答案为:(0,0)或(2,2 )或(-1,
)或(-1, )或(3,
)或(3, ).
).
点评:本题考查了全等三角形性质,勾股定理,含30度角的直角三角形性质的应用,注意要进行分类讨论啊.
 )或(-1,
)或(-1, )或(3,
)或(3, )
)分析:根据题意分为四种情况,画出图形,根据全等三角形性质和含30度角的直角三角形性质,勾股定理求出即可.
解答:∵点A的坐标是(2,0),∠ABO=30°,
∴OA=2,AB=2AO=4,由勾股定理得:OB=2
 ,
,分为四种情况:①当P和O重合时,符合条件,此时P的坐标是(0,0);
②

如图1,此时PB=OA=2,PA=OB=2
 ,
,即P的坐标是(2,2
 );
);③

如图2,过P作PM⊥OA于M,
则∠PAM=60°-30°=30°,
∴PM=
 AP=
AP= OB=
OB= ,
,AM=
 PM=3,
PM=3,∴OM=3-2=1,
∴P的坐标是(-1,
 );
);④

如图3,过P作PM⊥OA于M,
则∠PAM=180°-60°-60°=60°,
∴∠APM=30°,
∴AM=
 AP=
AP= OA=1,
OA=1,∴PM=
 AM=
AM= ,OM=1+2=3,
,OM=1+2=3,∴P的坐标是(3,
 ),
),故答案为:(0,0)或(2,2
 )或(-1,
)或(-1, )或(3,
)或(3, ).
).点评:本题考查了全等三角形性质,勾股定理,含30度角的直角三角形性质的应用,注意要进行分类讨论啊.

练习册系列答案
相关题目
 如图,直线AB与x轴交于点C,与反比例函数
如图,直线AB与x轴交于点C,与反比例函数 线AB、x轴、y轴交于点C、D、E.
线AB、x轴、y轴交于点C、D、E. 已知:如图,直线AB与x轴交于点A,与y轴交于点B.
已知:如图,直线AB与x轴交于点A,与y轴交于点B. 如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O逆时针旋转90°得到直线A1B1.
如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O逆时针旋转90°得到直线A1B1. 如图,直线AB与x轴、y轴分别交于点A、B,点A的坐标是(2,0),∠ABO=30°.在坐标平面内,是否存在点P(除点O外),使得△APB与△AOB全等.请写出所有符合条件的点P的坐标
如图,直线AB与x轴、y轴分别交于点A、B,点A的坐标是(2,0),∠ABO=30°.在坐标平面内,是否存在点P(除点O外),使得△APB与△AOB全等.请写出所有符合条件的点P的坐标