题目内容
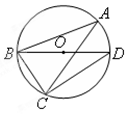
如图, △ABC中,AB=AC=3cm,BC=2cm,以AC为直径作半圆交AB于点D,交BC于点E,则图中阴影部分面积为 cm2.


根据圆周角定理得出DE=EC,进而得出阴影部分面积之和等于S△EBD,再利用相似三角形的判定与性质求出即可.
解答:解:连接DE,AE,

∵AB=AC=3cm,AC为直径,
∴∠B=∠C,AE⊥BC,
∴∠BAE=∠CAE,BE=EC=1cm,
∴ ,
,
∴DE=EC,
∴BE=DE,
∵∠B=∠C,
∴∠B=∠EDB,∠C=∠B,
∴△ABC∽△EBD,
∴ ,
,
∴ ,
,
∵EC=1cm,AC=3cm,
∴AE= ,
,
∴S△ABC= ×AE×BC=
×AE×BC= ×2
×2 ×2=2
×2=2 (cm 2),
(cm 2),
∴阴影部分面积=S△EBD= ×2
×2 =
= (cm 2),
(cm 2),
故答案为: .
.
解答:解:连接DE,AE,

∵AB=AC=3cm,AC为直径,
∴∠B=∠C,AE⊥BC,
∴∠BAE=∠CAE,BE=EC=1cm,
∴
 ,
,∴DE=EC,
∴BE=DE,
∵∠B=∠C,
∴∠B=∠EDB,∠C=∠B,
∴△ABC∽△EBD,
∴
 ,
,∴
 ,
,∵EC=1cm,AC=3cm,
∴AE=
 ,
,∴S△ABC=
 ×AE×BC=
×AE×BC= ×2
×2 ×2=2
×2=2 (cm 2),
(cm 2),∴阴影部分面积=S△EBD=
 ×2
×2 =
= (cm 2),
(cm 2),故答案为:
 .
.
练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
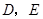 分别是半径
分别是半径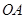 和
和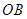 的中点
的中点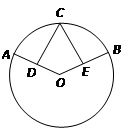
 CD=CE.
CD=CE.
 B.
B.  C.
C.  D. 4
D. 4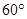 ,半径为1,将它沿着箭头方向无滑动滚动到
,半径为1,将它沿着箭头方向无滑动滚动到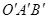 位置,
位置,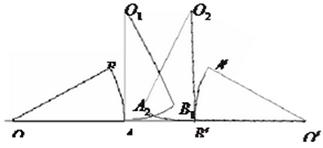
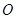 到
到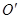 的路径是
的路径是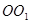
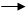
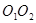
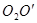 ;
;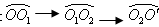 ;
;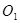
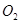 段上运动路线是线段
段上运动路线是线段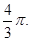
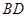 为⊙O的直径,∠A=35°,则
为⊙O的直径,∠A=35°,则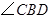 的度数为 。
的度数为 。