题目内容
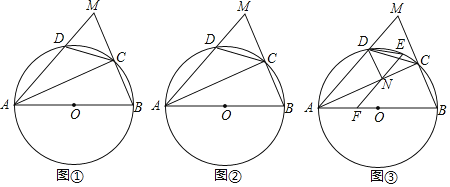
【题目】已知:在![]() 中,C、D分别为BM、AM上的点,四边形ABCD内接于
中,C、D分别为BM、AM上的点,四边形ABCD内接于![]() ,连接AC,
,连接AC,![]() ;
;
![]() 如图
如图![]() ,求证:弧
,求证:弧![]() 弧BD;
弧BD;
![]() 如图
如图![]() ,若AB为直径,
,若AB为直径,![]() ,求
,求![]() 值;
值;
![]() 如图
如图![]() ,在
,在![]() 的条件下,E为弧CD上一点
的条件下,E为弧CD上一点![]() 不与C、D重合
不与C、D重合![]() ,F为AB上一点,连接EF交AC于点N,连接DN、DE,若
,F为AB上一点,连接EF交AC于点N,连接DN、DE,若![]() ,
,![]() ,
,![]() ,求AN的长.
,求AN的长.
【答案】(1)详见解析;(2)![]() (3)
(3)![]()
【解析】
![]() 证明弧
证明弧![]() 弧BD可以转化证明
弧BD可以转化证明![]()
![]() 是直径可知三角形ABD是等腰直角三角形,从而得出
是直径可知三角形ABD是等腰直角三角形,从而得出![]() ,利用
,利用![]() 的特殊性构造直角三角形DCG,结合
的特殊性构造直角三角形DCG,结合![]() ,可以求出
,可以求出![]() ,进而求出
,进而求出![]()
![]() 为了求AN,可以过点N作
为了求AN,可以过点N作![]() 于点M,求出MN,AM,即可求出
于点M,求出MN,AM,即可求出![]() 因为P是BD的中点,所以连结OP,根据垂径定理可以得出
因为P是BD的中点,所以连结OP,根据垂径定理可以得出![]() ,根据
,根据![]() 可得
可得![]() ,从而得到矩形OPLH,结合矩形的性质,可以得出OH,EH的长度关系,在利用勾股定理建立方程,可求出HO,进而求出MN,AM,最终得出AN的长度.
,从而得到矩形OPLH,结合矩形的性质,可以得出OH,EH的长度关系,在利用勾股定理建立方程,可求出HO,进而求出MN,AM,最终得出AN的长度.
![]() ,
,![]()
![]() ,
,
又![]()
![]() ,
,
![]() 弧
弧![]() 弧BD
弧BD
![]() 作
作![]() 于点G,连结
于点G,连结![]() 如图
如图![]()
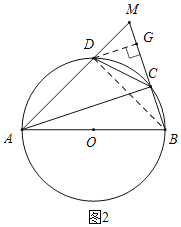
![]() 为直径
为直径
弧![]() 弧
弧![]()
![]() ,
,
又![]()
![]() ,
,
又![]()
![]() ,
,
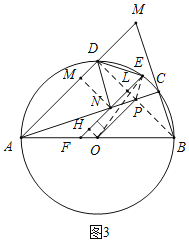
![]() 连结BD交AC,EF分别为点P,点L,连结OP,OE,PE,再作
连结BD交AC,EF分别为点P,点L,连结OP,OE,PE,再作![]() 于点H,
于点H,![]() 于点
于点![]() 如图3所示
如图3所示![]()
![]() ,
,![]() ,
,
![]() ,
,
由![]() 得
得![]()
![]() ,
,
即P为BD的中点
![]() ,
,
![]() 四边形OPLH为矩形
四边形OPLH为矩形
设![]() ,则
,则![]() .
.
又![]()
![]() 垂直平分NE
垂直平分NE
![]() ,
,
又![]() 为等腰直角三角形
为等腰直角三角形
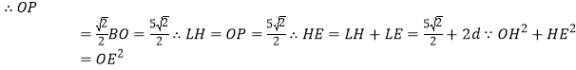
![]() ,
,
解得![]()
![]() ,
,
![]() .
.

练习册系列答案
相关题目