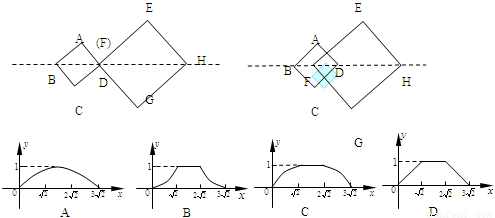
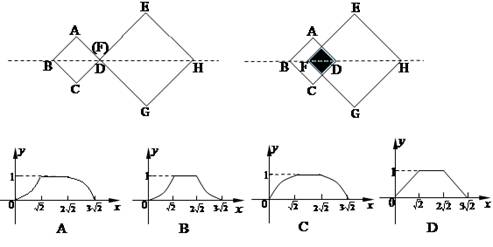
题目内容
 如图,设点P是边长为a的正三角形ABC的边BC上一点,过点P作PQ⊥AB,垂足为Q,延长QP交AC的延长线于点R.当点P在何处时,△BPQ与△CPR的面积之和取最大(小)值?并求出最大(小)值.
如图,设点P是边长为a的正三角形ABC的边BC上一点,过点P作PQ⊥AB,垂足为Q,延长QP交AC的延长线于点R.当点P在何处时,△BPQ与△CPR的面积之和取最大(小)值?并求出最大(小)值.分析:首先设PB=x,由∠B=60°,得:BQ=
,PQ=
,从而有PC=CR=a-x,进而表示出S=
x2+
(a-x)2,进而利用二次函数最值求法得出即可.
| x |
| 2 |
| ||
| 2 |
| ||
| 8 |
| ||
| 4 |
解答: 解:在Rt△BPQ中,设PB=x,由∠B=60°,得:
解:在Rt△BPQ中,设PB=x,由∠B=60°,得:
BQ=
,PQ=
,从而有PC=CR=a-x,
∴△BPQ与△CPR的面积之和为:
S=
x2+
(a-x)2=
(x-
a)2+
a2,
∵0≤x≤a,
∴当x=0时,S取最大值
a2,
当x=
a时,S取最小值
a2.
 解:在Rt△BPQ中,设PB=x,由∠B=60°,得:
解:在Rt△BPQ中,设PB=x,由∠B=60°,得:BQ=
| x |
| 2 |
| ||
| 2 |
∴△BPQ与△CPR的面积之和为:
S=
| ||
| 8 |
| ||
| 4 |
3
| ||
| 8 |
| 2 |
| 3 |
| ||
| 12 |
∵0≤x≤a,
∴当x=0时,S取最大值
| ||
| 4 |
当x=
| 2 |
| 3 |
| ||
| 12 |
点评:此题主要考查了二次函数最值求法和三角形面积求法,表示出S与x的函数关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
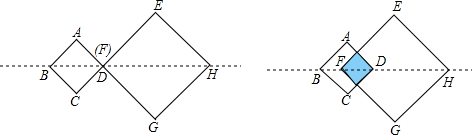
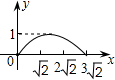
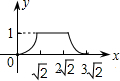
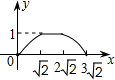
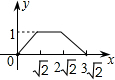
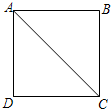 (2013•槐荫区二模)如图,四边形ABCD是边长为2的正方形,现有两点E、F,分别从点D、点A同时出发,点E沿线段DA以1个单位长度每秒的速度向点A运动,点F沿折线A-B-C以2个单位长度每秒的速度向点C运动.设点E离开点D的时间为t秒.
(2013•槐荫区二模)如图,四边形ABCD是边长为2的正方形,现有两点E、F,分别从点D、点A同时出发,点E沿线段DA以1个单位长度每秒的速度向点A运动,点F沿折线A-B-C以2个单位长度每秒的速度向点C运动.设点E离开点D的时间为t秒.