题目内容
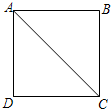 (2013•槐荫区二模)如图,四边形ABCD是边长为2的正方形,现有两点E、F,分别从点D、点A同时出发,点E沿线段DA以1个单位长度每秒的速度向点A运动,点F沿折线A-B-C以2个单位长度每秒的速度向点C运动.设点E离开点D的时间为t秒.
(2013•槐荫区二模)如图,四边形ABCD是边长为2的正方形,现有两点E、F,分别从点D、点A同时出发,点E沿线段DA以1个单位长度每秒的速度向点A运动,点F沿折线A-B-C以2个单位长度每秒的速度向点C运动.设点E离开点D的时间为t秒.(1)t=
| 2 |
| 3 |
(2)当t为何值时,线段EF与DC平行;
(3)当1≤t<2时,设EF与AC相交于点M,连接DM并延长交AB于点N,求
| AN |
| NB |
分析:(1)根据运动的过程求得AE、AF的长即可作出判断;
(2)线段EF与DC平行,则F一定在边BC上,且DE=CF,即四边形EFCD为矩形,利用t表示出DE和CF,即可得到一个关于t的方程,从而求得;
(3)易证△AME∽△CMF,△AMN∽△CMD,根据相似三角形的对应边的比相等即可求解.
(2)线段EF与DC平行,则F一定在边BC上,且DE=CF,即四边形EFCD为矩形,利用t表示出DE和CF,即可得到一个关于t的方程,从而求得;
(3)易证△AME∽△CMF,△AMN∽△CMD,根据相似三角形的对应边的比相等即可求解.
解答:解:(1)t=
时,
DE=
,AF=
×2=
,
∵四边形ABCD是边长为2的正方形,
∴∠DAB=90°,AE=2-
=
,
∴AE=AF,
∴△AEF是等腰直角三角形.
(2)四边形ABCD是边长为2的正方形,
∴AD=BC=2,
当点F运动到边BC上且AE=BF时,
则有DE=CF,
∴四边形EFCD为矩形,
∴EF∥CD,
∵AE=2-t,BF=2t-2,
∴2-t=2t-2,
∴t=
,
∴t=
时线段EF与DC平行.
(3)由(2)知AE=2-t,
∵CF=4-2t,
∴
=
=
,
∵四边形ABCD是正方形,
∴AD∥BC,AB∥DC,
∴△AME∽△CMF,△AMN∽△CMD,
∴
=
=
,
∴
=
=
,
∴AN=
AB,
∴
=1.
| 2 |
| 3 |
DE=
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
∵四边形ABCD是边长为2的正方形,
∴∠DAB=90°,AE=2-
| 2 |
| 3 |
| 4 |
| 3 |
∴AE=AF,
∴△AEF是等腰直角三角形.
(2)四边形ABCD是边长为2的正方形,
∴AD=BC=2,
当点F运动到边BC上且AE=BF时,
则有DE=CF,
∴四边形EFCD为矩形,
∴EF∥CD,
∵AE=2-t,BF=2t-2,
∴2-t=2t-2,
∴t=
| 4 |
| 3 |
∴t=
| 4 |
| 3 |
(3)由(2)知AE=2-t,
∵CF=4-2t,
∴
| AE |
| CF |
| 2-t |
| 4-2t |
| 1 |
| 2 |
∵四边形ABCD是正方形,
∴AD∥BC,AB∥DC,
∴△AME∽△CMF,△AMN∽△CMD,
∴
| AM |
| CM |
| AE |
| CF |
| 1 |
| 2 |
∴
| AN |
| CD |
| AM |
| CM |
| 1 |
| 2 |
∴AN=
| 1 |
| 2 |
∴
| AN |
| NB |
点评:本题考查了正方形的性质、矩形的判定与性质、相似三角形的判定与性质的综合应用,正确求得
=2是关键.
| AE |
| CF |

练习册系列答案
相关题目
 (2013•槐荫区二模)如图,直线y=-
(2013•槐荫区二模)如图,直线y=-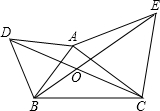 (2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是
(2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是 (2013•槐荫区二模)如图,在△ABC中AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分的面积是
(2013•槐荫区二模)如图,在△ABC中AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分的面积是