��Ŀ����
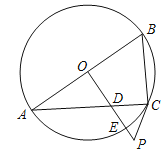
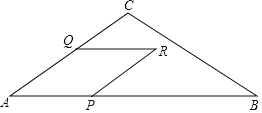
����Ŀ����ͼ���ڡ�ABC�У�AC��BC��5��AB��8����P��AB�ϣ���Q��AC��AC���ӳ����ϣ�AQ��AP����AP��AQΪ�ڱ�������APRQ����AP�ij�Ϊx������APRQ���ABC��Ӱ����ͼ�ε����Ϊy(ƽ����λ)��
(1)��sinA��ֵ.
(2)��xΪ��ֵʱ����R����BC��.
(3)������APRQ���ABC�ص����ֵ�ͼ��Ϊ�ı���ʱ����y��x�ĺ�����ϵʽ.
(4)ֱ��д����xΪ��ֵʱ�����������ζ����ֱ��ͬʱ�����Ρ������ε�������ȷ�.
���𰸡�(1)sinA��![]() ��(2)x��
��(2)x��![]() ��(3)y=��
��(3)y=��![]() x2+3x+8��(4)����������x��ֵΪ
x2+3x+8��(4)����������x��ֵΪ![]() ��
��![]() .
.
��������
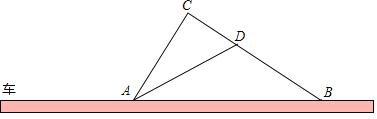
(1)��ͼ1�У���CD��AB��D.���ݵ��������ε������Լ����ɶ������CD���ɽ������.
(2)��QR��BC���ɵ�![]() ��
��![]() ���ɴ˹������̼��ɽ������.
���ɴ˹������̼��ɽ������.
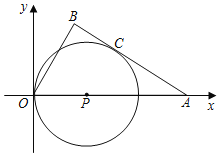
(3)���������Σ��ٵ�0��x��![]() ʱ���ص�����������APRQ.����ͼ3�У���5��x��8ʱ���ص��������ı���APMC����MH��PB��H.�ֱ���⼴��.
ʱ���ص�����������APRQ.����ͼ3�У���5��x��8ʱ���ص��������ı���APMC����MH��PB��H.�ֱ���⼴��.
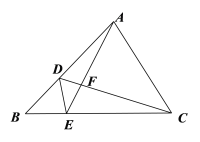
(4)���������Σ�����AR��PQ���ڵ�O������O�ڡ�ABC������BM��ʱ����������.��ͼ4�У���OH��AB��AC��H.��ͼ5�У�����O��������AD��ʱ����������.�ֱ�����ƽ���߷��߶γɱ����������������̼��ɽ������.
�⣺(1)��ͼ1�У���CD��AB��D.
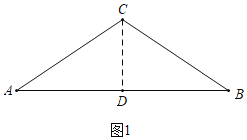
��CA��CB��5��CD��AB��
��AD��DB��4����ADC��90����
��CD��![]() ��
��![]() ��3.
��3.
��sinA��![]() ��
��![]() ��
��
(2)��ͼ2�У�����R����BC��ʱ��
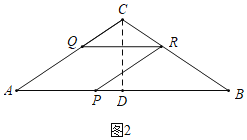
��QR��BC��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��x��![]() .
.
(3)�ٵ�0��x��![]() ʱ���ص�����������APRQ��S��PAAQsinA��x
ʱ���ص�����������APRQ��S��PAAQsinA��x![]() x��
x��![]() x2.
x2.
����ͼ3�У���5��x��8ʱ���ص��������ı���APMC����MH��PB��H.
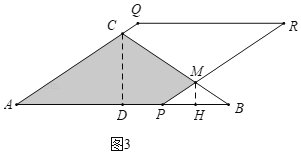
��Rt��MPH��PH��BH��![]() ��
��
MH��PHtan��MPH��![]()
![]()
S��S��ABC��S��PBM��![]() ��8��5��
��8��5��![]() (8��x)
(8��x)![]()
![]() ����
����![]() x2+3x+8.
x2+3x+8.
(4)����AR��PQ���ڵ�O������O�ڡ�ABC������BM��ʱ����������.��ͼ4�У���OH��AB��AC��H.
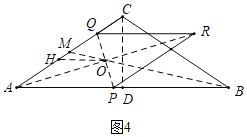
��OQ��OP��OH��PA��
��AH��HQ��![]() x��OH��
x��OH��![]() PA��
PA��![]() x��
x��
��OH��AB��
��![]() ��
��![]() ��
��
��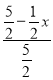 ��
��![]() ��
��
���x��![]() .
.
��ͼ5�У�����O��������AD��ʱ����������.
![]()
��OH��AD��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
���x��![]() ��
��
��������������������x��ֵΪ![]() ��
��![]() .
.

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�