Question

在?ABCD中，对角线AC、BD相交于点O，且AB≠AD，则下列四个结论①AC⊥BD，②AB=CD，③BO=OD，④∠BAD=∠BCD中不正确的是

①

 （填序号）

Answer 1

分析：根据平行四边形的性质可知，平行四边形的对边相等，对角线互相平分，两组对角分别相等，由此判断出选项②③④正确．再由平行四边形对角线互相平分可知OB=OD，利用反证法假设AC垂直BD，再加上一条公共边，得到两个三角形的全等，由全等三角形的对应边相等得出AB=AD，与已知AB≠AD矛盾，故AC不能与BD垂直，所以判断出选项①错误．

解答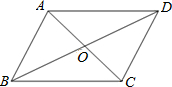：解：∵四边形ABCD为平行四边形，
∴AB=CD，则选项②正确；
又根据平行四边形的对角线互相平分，
∴BO=OC，则选项③正确；
又∵四边形ABCD为平行四边形，
∴AB∥CD，AD∥BC，
∴∠ABC+∠BCD=180°，∠BAD+∠ABC=180°，
∴∠BAD=∠BCD，则选项④正确；
由BO=OD，假设AC⊥BD，
又∵OA=OA，
∴△ABO≌△ADO，
∴AB=AD与已知AB≠AD矛盾，
∴AC不垂直BD，则选项①错误．
故答案为①．

点评：本题考查学生对平行四边形性质的熟练掌握及应用，会用反证法进行证明，是一道中档题．