题目内容
 如图,在△ABC中,AB=AC,D是BC上的任意一点.
如图,在△ABC中,AB=AC,D是BC上的任意一点.(1)过A、B、D三点作⊙O,交线段AC于点E(用直尺和圆规作图,保留作图痕迹,不写作法);
(2)若
 |
| DE |
 |
| DB |
(3)在(2)的条件下,若AB=5,BC=6,求AE的长.
考点:作图—复杂作图
专题:
分析:(1)作AB与BD的垂线,交于点O,点O就是△ABD的外心,⊙O交线段AC于点E;
(2)连结DE,根据圆内接四边形的性质,等腰三角形的性质,即可得到AD是等腰三角形ABC底边上的高线,从而证明AB是⊙O的直径;
(3)连结BE,根据勾股定理得到关于AE的方程,解方程即可求解.
(2)连结DE,根据圆内接四边形的性质,等腰三角形的性质,即可得到AD是等腰三角形ABC底边上的高线,从而证明AB是⊙O的直径;
(3)连结BE,根据勾股定理得到关于AE的方程,解方程即可求解.
解答:(1)解:如图1所示:
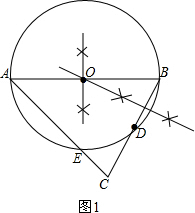
(2)证明:如图2,连结DE,AD.
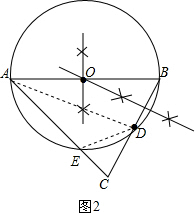
∵过A、B、D三点作⊙O,交线段AC于点E,
∴A、B、D、E四点共圆,
∴∠DEC=∠ABC,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠DEC=∠ACB,
∴DE=CD,
∵
=
,
∴DE=BD,
∴CD=BD,
∴AD⊥BC,
∴AB是⊙O的直径;
(3)如图3,连结BE.
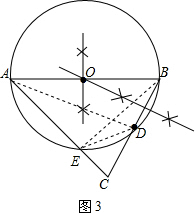
∵AB是⊙O的直径,
∴BE⊥AC,
由勾股定理可得,AB2-AE2=BC2-(AC-AE)2,即52-AE2=62-(5-AE)2,
解得AE=1.4.
故AE的长是1.4.

(2)证明:如图2,连结DE,AD.

∵过A、B、D三点作⊙O,交线段AC于点E,
∴A、B、D、E四点共圆,
∴∠DEC=∠ABC,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠DEC=∠ACB,
∴DE=CD,
∵
 |
| DE |
 |
| DB |
∴DE=BD,
∴CD=BD,
∴AD⊥BC,
∴AB是⊙O的直径;
(3)如图3,连结BE.

∵AB是⊙O的直径,
∴BE⊥AC,
由勾股定理可得,AB2-AE2=BC2-(AC-AE)2,即52-AE2=62-(5-AE)2,
解得AE=1.4.
故AE的长是1.4.
点评:考查了作图-复杂作图,线段垂直平分线的作法,圆内接四边形的性质,等腰三角形的性质,勾股定理,方程思想的应用.

练习册系列答案
相关题目
如图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,按此规律,则第10个图形中基础图形的个数是( )


| A、27 | B、30 | C、31 | D、60 |
⊙O的半径为4,直线l与⊙O相切,则O到直线l的距离是( )
| A、小于4 | B、等于4 |
| C、大于4 | D、无法确定 |
下列事件属于随机事件的是( )
| A、任意画一个三角形,其内角和是180° |
| B、掷一次骰子,向上的一面的点数是7 |
| C、从只有红球的袋子中,摸出1个白球 |
| D、打开电视,电视正在播放新闻节目 |
 如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,
如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°, 如图,长方形纸片ABCD中,已知AD=8,AB=6,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,则CE的长为
如图,长方形纸片ABCD中,已知AD=8,AB=6,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,则CE的长为 三角形纸片ABC中,∠A=82°,∠B=63°,若将纸片的角C折叠到如图的位置,点C落在△ABC外部,则∠α﹑∠β之间的关系是
三角形纸片ABC中,∠A=82°,∠B=63°,若将纸片的角C折叠到如图的位置,点C落在△ABC外部,则∠α﹑∠β之间的关系是