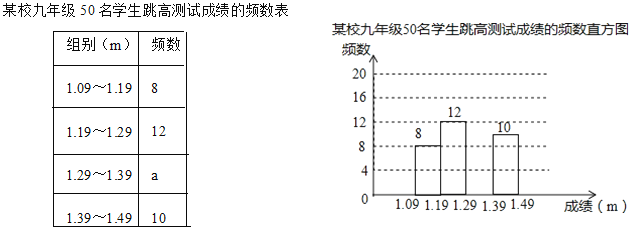
题目内容
【题目】已知二次函数![]() .
.
(1)该二次函数的顶点坐标为__________;
(2)该函数的图象与![]() 轴的交点坐标为__________;
轴的交点坐标为__________;
(3)用五点法画函数图象
| … | … | |||||
| … | … |
(4)当![]() 时,则
时,则![]() 的取值范围是__________;
的取值范围是__________;
(5)将该抛物线绕顶点旋转180°,所得函数的解析式为__________;
(6)抛物线![]() 与
与![]() 轴有且仅有一个交点,则
轴有且仅有一个交点,则![]() __________.
__________.

【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() (3)函数图象见解析;(4)
(3)函数图象见解析;(4)![]() ;(5)
;(5)![]() ;(6)4.
;(6)4.
【解析】
(1)将二次函数的解析式化成顶点式即可得;
(2)令![]() ,求解一元二次方程即可得;
,求解一元二次方程即可得;
(3)先列出图象上的五个点,再顺次连接即可画出函数图象;
(4)根据(3)的图象即可得;
(5)先根据旋转的性质可得顶点坐标不变,从而可得新二次函数的顶点式,再求出点![]() 绕顶点旋转
绕顶点旋转![]() 所得点的坐标,然后代入求解即可得;
所得点的坐标,然后代入求解即可得;
(6)根据二次函数![]() 的图象可知,将其向上平移4个单位长度所得的图象与
的图象可知,将其向上平移4个单位长度所得的图象与![]() 轴有且仅有一个交点,由此即可得出k的值.
轴有且仅有一个交点,由此即可得出k的值.
(1)将二次函数![]() 化成顶点式为
化成顶点式为![]()
则该二次函数的顶点坐标为![]()
故答案为:![]() ;
;
(2)令![]() 得
得![]()
解得![]()
则该函数的图象与![]() 轴的交点坐标为
轴的交点坐标为![]() ,
,![]()
故答案为:![]() ,
,![]() ;
;
(3)根据二次函数的解析式,列出五个点(注:五个点对称列出即可,不刻意要求特殊点
),如下表所示:
| … | -3 | -2 | -1 | 0 | 1 | … |
| … | 0 | -3 | -4 | -3 | 0 | … |
利用五点法画函数图象如下:
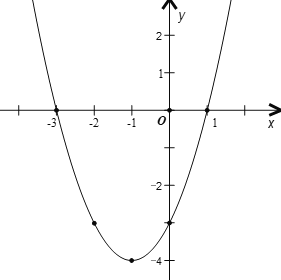
(4)由(3)所画的函数图象可知,当![]() 时,
时,![]()
故答案为:![]() ;
;
(5)如图,点B绕点A旋转![]() 的对应点为点D
的对应点为点D
由旋转的性质得:新二次函数的顶点坐标仍为![]()
设新二次函数的解析式为![]()
由点![]() 可知,
可知,![]()
由旋转的性质可知,![]()
在![]() 和
和![]() 中,
中,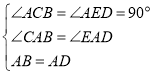
![]()
![]()
![]()
![]()
将![]() 代入
代入![]() 得,
得,![]()
解得![]()
则新二次函数的解析式为![]()
故答案为:![]() ;
;
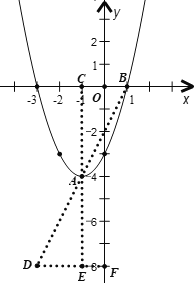
(6)由函数图象的平移规律可知,抛物线![]() 是由二次函数
是由二次函数![]() 向上
向上![]() 或向下
或向下![]() 平移得到的
平移得到的
由二次函数![]() 的图象可知,将其向上平移4个单位长度所得的图象与
的图象可知,将其向上平移4个单位长度所得的图象与![]() 轴有且仅有一个交点
轴有且仅有一个交点
则![]()
故答案为:4.