题目内容
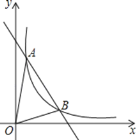
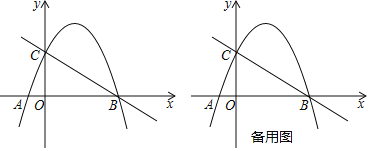
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,其中点B的坐标为(4,0),与y轴交于点C(0,2).
x2+bx+c与x轴交于点A,B,其中点B的坐标为(4,0),与y轴交于点C(0,2).
(1)求抛物线y=﹣![]() +bx+c和直线BC的函数表达式;
+bx+c和直线BC的函数表达式;
(2)点P是直线BC上方的抛物线上一个动点,当点P到直线BC的距离最大时,求点P的坐标;
(3)连接点O与(2)中求出的点P,交直线BC于点D,点N是直线BC上的一个动点,连接ON,作DF⊥ON于点F,点F在线段ON上,当OD=![]() DF时,请直接写出点N的坐标.
DF时,请直接写出点N的坐标.
【答案】(1)![]() ,
,![]() ;(2)P(2,3);(3)
;(2)P(2,3);(3)![]() 或
或![]()
【解析】
(1)分别利用待定系数法求解即可;
(2)作PQ⊥x轴交BC于Q,连结PC,PB,表示出PQ,根据PQ最大时,S△PBC最大,此时,P到BC的距离最大进行求解;
(3)分N在D的右边和左边两种情况讨论,可得△DON~△DBO,然后求出DN,BN,从而进一步求出N的坐标.
解:(1)将![]() 代入
代入![]() ,
,
得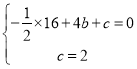 ,解得
,解得 ![]() ,
,
∴![]() ;
;
设BC:y=kx+m,
则![]() ,解得:
,解得: ,
,
∴![]() ;
;
(2)作PQ⊥x轴交BC于Q,连结PC,PB

设![]() ,
,![]() ,
,
∴![]() ,
,
∴当x=2,PQ最大值为2,
∵![]() ,
,
∴当PQ最大时,S△PBC最大,此时,P到BC的距离最大,
∴P(2,3);
(3)由(2)得P(2,3)
∴直线![]() ,
,
联立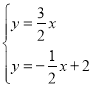 ,解得
,解得 ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ ;
;
①当N在D的右侧时,如图,作NG⊥OB于G,

∵OC=2,BC=![]() ,
,
∴![]() ,
,
∴∠DON=∠OBC,
∴△DON~△DBO,
∴![]() ,
,
∴OD2=DNBD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②当N在D的左侧时,
同理可得:![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
综上所述:![]() 或
或![]() .
.

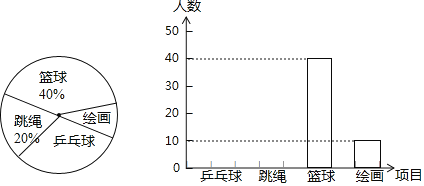
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?