��Ŀ����
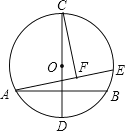
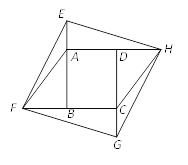
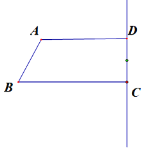
����Ŀ����ͼ���ı���ABCD�У�AD��BC����ADC=90����AD=4��CD=2��BC=5����E��BC������B��C�˶�(�����C�غ�)������AE,����E��AE�Ĵ��߽�ֱ��CD��F�㣮��BE�ij�Ϊ![]() ��CF�ij�Ϊ
��CF�ij�Ϊ![]() ��
��
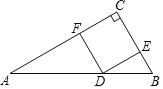
(1) ��![]() ��ֵ
��ֵ
(2) ��![]() �ij���(�ú�
�ij���(�ú�![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
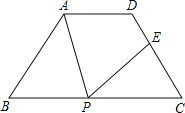
(3) ����AF,�ڵ�E�˶��Ĺ����У���![]() ������
������![]() ���λ��Ҳ��֮�仯,̽����
���λ��Ҳ��֮�仯,̽����![]() ����ʲô����������
����ʲô����������![]() �����ı���ABCD�ı��ϻ�����.
�����ı���ABCD�ı��ϻ�����.
���𰸡�(1)![]() ��(2)
��(2) ![]() ��
��![]() ��(3)
��(3)![]() ��
�� ![]()
��������
��1����ͼ����AE1��BC������AD=4��CD=2,�õ�AE1=CD=2,BE1=BC-E1C=1���ʿ����![]() ��ֵ��
��ֵ��
��2��E��ȡ���������λ��E1,E2,AE1��BC��AE2��DE2����ADΪֱ����Բ��BC������E2,�ٸ���ͼ�η�0��x��1����1��x��5���������������CEF�ס�E1AE�������߶γɱ����õ�x��y�Ĺ�ϵʽ��
��3����ͼ�����ݡ�AEFΪֱ�������Σ���AEF������MΪAF�е㣬�ٷ�E��BE1����E��E1C�����������������.
��1����ͼ����AE1��BC��
��AD=4��CD=2,
��AE1=CD=2,BE1=BC-E1C=1��
��![]() =
=![]() =2;
=2;
��2��E��ȡ���������λ��E1,E2,AE1��BC��AE2��DE2����ADΪֱ����Բ��BC������E2,
��0��x��BE1ʱ����0��x��1ʱ��EE1=1-x,EC=5-x��AE1=2��
�ߡ�AEF=90����
���AEE1+��FEC=90����
�֡�AEE1+��E1AE=90����
���FEC=��E1AE
�֡�AE1E=��ECF=90����
����CEF�ס�E1AE��
��![]()
��![]()
�����![]()
��E��CE1��ʱ������1��x��5ʱ��EE1=x-1,EC=5-x��AE1=2��
ͬ���ɵ���CEF�ס�E1AE��
��![]()
��![]()
�����![]()
��3����ͼ�����ݡ�AEFΪֱ�������Σ���AEF������MΪAF�е㣬
��E��BE1�ϣ���ͼ������M��BC�ϣ���ʱM��E2�غϣ�AM=MF��
��AE1��DF����CF=AE1=2
��EE2=AE2=AE1��cos45��=2![]()
���ʱx=BE=BE2- EE2=3-2![]()
�൱![]() ʱ��CF��AE1������
ʱ��CF��AE1������![]() �����ı���ABCD�ı��ϻ����⣻
�����ı���ABCD�ı��ϻ����⣻
��E��E1C�ϣ���x=3ʱ����ͼ��M��AD�е㴦������![]() �����ı���ABCD��AD���ϣ�����M�㶼���ı���ABCD�ڲ���
�����ı���ABCD��AD���ϣ�����M�㶼���ı���ABCD�ڲ���
���ϣ�![]() ��
�� ![]() ����
����![]() �����ı���ABCD�ı��ϻ�����.
�����ı���ABCD�ı��ϻ�����.