题目内容
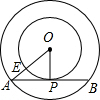
如图，△ABC中，AB=4，AC=2，BC=2
，以BC为直径的半圆交AB于点D，以A为圆心，AC为半径的
扇形交AB于点E．
（1）以BC为直径的圆与AC所在的直线有何位置关系？请说明理由；
（2）求图中阴影部分的面积（结果可保留根号和π）．
| 3 |
扇形交AB于点E．（1）以BC为直径的圆与AC所在的直线有何位置关系？请说明理由；
（2）求图中阴影部分的面积（结果可保留根号和π）．
（1）相切．（1分）
理由：∵22+（2
）2=16=42，
∴AC2+BC2=AB2．
∴∠ACB=90°．
∴以BC为直径的圆与AC所在的直线相切．（4分）
（2）∵Rt△ABC中，cosA=
=
．
∴∠A=60°．（5分）
∴S阴影=S半圆-（S△ABC-S扇形ACE）
=
π（
）2-（
×2×2
-
π×22）=
-2
．（8分）
理由：∵22+（2
| 3 |
∴AC2+BC2=AB2．
∴∠ACB=90°．
∴以BC为直径的圆与AC所在的直线相切．（4分）
（2）∵Rt△ABC中，cosA=
| AC |
| AB |
| 1 |
| 2 |
∴∠A=60°．（5分）
∴S阴影=S半圆-（S△ABC-S扇形ACE）
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 60 |
| 360 |
| 13π |
| 6 |
| 3 |
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
