题目内容
在?ABCD中,M为CD的中点,如DC=2AD,则AM、BM夹角度数是
- A.90°
- B.95°
- C.85°
- D.100°
A
分析:如图,由四边形ABCD是平行四边形,可得AB∥CD,AD=BC;由M为CD的中点,如DC=2AD,易得AD=DM=CM=BC,所以∠DAM=∠DMA,∠MBC=∠BMC;又因为∠MAB=∠DMA,∠MBA=∠BMC,易得∠MAB+∠MBA=90°,所以∠AMB=90°.
解答: 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,
∴∠DAB+∠ABC=180°,∠MAB=∠DMA,∠MBA=∠BMC,
∵M为CD的中点,如DC=2AD,
∴AD=DM=CM=BC,
∴∠DAM=∠DMA,∠MBC=∠BMC,
∴∠MAB+∠MBA=90°,
∴∠AMB=90°.
∴AM、BM夹角度数是90°.
点评:此题考查了平行四边形的性质与等腰梯形的判定与性质.此题有一定的综合性,但难度不大.解题时要注意数形结合思想的应用.
分析:如图,由四边形ABCD是平行四边形,可得AB∥CD,AD=BC;由M为CD的中点,如DC=2AD,易得AD=DM=CM=BC,所以∠DAM=∠DMA,∠MBC=∠BMC;又因为∠MAB=∠DMA,∠MBA=∠BMC,易得∠MAB+∠MBA=90°,所以∠AMB=90°.
解答:
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,AD=BC,
∴∠DAB+∠ABC=180°,∠MAB=∠DMA,∠MBA=∠BMC,
∵M为CD的中点,如DC=2AD,
∴AD=DM=CM=BC,
∴∠DAM=∠DMA,∠MBC=∠BMC,
∴∠MAB+∠MBA=90°,
∴∠AMB=90°.
∴AM、BM夹角度数是90°.
点评:此题考查了平行四边形的性质与等腰梯形的判定与性质.此题有一定的综合性,但难度不大.解题时要注意数形结合思想的应用.

练习册系列答案
相关题目
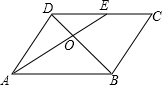 如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB等于( )cm2.
如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB等于( )cm2.| A、24 | B、36 | C、48 | D、144 |
 14、如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为
14、如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为 如图,在?ABCD中,E为CD的中点,AE交BD于点F,则△EFD和△AFB的面积比为
如图,在?ABCD中,E为CD的中点,AE交BD于点F,则△EFD和△AFB的面积比为 如图,在?ABCD中,BD为对角线,EF垂直平分BD分别交AD、BC的于点E、F,交BD于点O.
如图,在?ABCD中,BD为对角线,EF垂直平分BD分别交AD、BC的于点E、F,交BD于点O.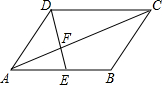 如图,在?ABCD中,E为AB的中点,DE交AC于F,△AEF∽
如图,在?ABCD中,E为AB的中点,DE交AC于F,△AEF∽