Question

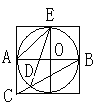
如图，AB是⊙O的直径，弦CD⊥AB，垂足为点P，若AB=2，AC=.

求：（1）∠A的度数；（2）的长；（3）弓形CBD的面积.

Answer 1

（1）30°；（2）；（3）．

试题分析：（1）过O作OE⊥AC，由垂径定理可得AE的长，再用三角函数即可求得∠A的度数；
（2）由∠A得度数得出对应圆心角∠COB的度数，由垂径定理得∠DOB=∠COB，由此得到∠COD的度数，用弧长公式即可求出弧长；
（3）由公式：弓形CBD的面积=扇形COD的面积－△COD的面积，即可求出弓形面积．
试题解析：(1)过O作OE⊥AC，∵AC=，∴AE=EC=，在Rt△AEO中，cos∠A=，∴∠A=30°；

（2）连结OC，OD，∵∠A=30°，∴∠COB=60°，∵AB是⊙O的直径，弦CD⊥AB，∴弧BC=弧BD，∴∠DOB=∠COB=60°，∴∠COD=120°，∵AB=2，∴OC=OB=×2=1，∴的长=；
（3）∵∠COB=60°，OP⊥CD，∴∠OCP=30°，∵OC=1，∴OP=，CP=，∴CD=，∴弓形CBD的面积=扇形COD的面积－△COD的面积==．