题目内容
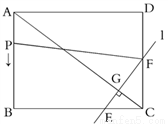
如图,在矩形ABCD中,AB=12cm,BC=16cm,连接AC. 点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时,直线l从点C出发,沿CA以1cm/s的速度向点A匀速运动,直线l分别交BC,CD于点E,F,且EF⊥AC,垂足为G,当点P停止运动时,直线l也停止运动,连接PF.设点P的运动时间为t(s)(0<t<12).
(1)当t为何值时,四边形PBCF是矩形?
(2)设四边形PBEF的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PBEF ∶ S矩形ABCD=181∶384若存在,求出t的值;若不存在,请说明理由. (提示:1722=29584)
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目


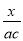 ,
, 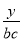 ;(2)
;(2)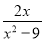 ,
, 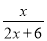 .
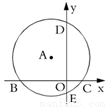
.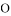 的半径长为
的半径长为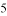 ,若点
,若点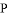 在⊙
在⊙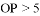 B.
B. 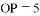 C.
C. 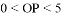 D.
D. 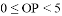
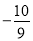 ______
______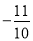 (填“
(填“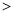 ”或“
”或“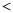 ”)
”)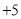 分,某同学得71分,则应记为( )
分,某同学得71分,则应记为( )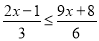 .
.
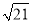 B. 4
B. 4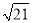 C. 8 D. 16
C. 8 D. 16 .
.