题目内容
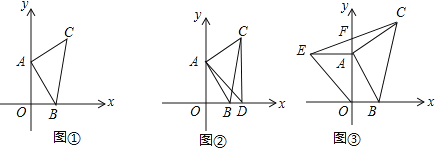
【题目】已知:点A在射线CE上,∠C=∠D.
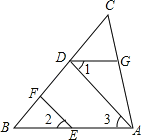
(1)如图1,若AC∥BD,求证:AD∥BC;
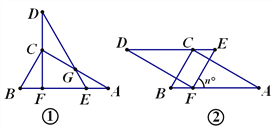
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

【答案】(1)详见解析;(2)∠EAD+2∠C=90°,证明详见解析;(3)99°.
【解析】试题分析: ![]() 根据AC∥BD,得到
根据AC∥BD,得到![]() 又
又![]() 根据等量代换得到
根据等量代换得到![]() 即可判定AD∥BC;
即可判定AD∥BC;
![]()
![]() 根据外角的性质得到
根据外角的性质得到![]() 又因为
又因为![]()
根据三角形的内角和得到![]() 又
又![]() 即可得到它们的关系.
即可得到它们的关系.
![]() 设
设![]() 则
则![]()
![]() 根据平行线的性质
根据平行线的性质![]() 根据第
根据第![]() 问的结论求出
问的结论求出![]() 的度数,根据内角和求出
的度数,根据内角和求出![]() 的度数.
的度数.
试题解析:
(1)如图1,

∵AC∥BD,
![]()
又∵![]()
![]()
∴AD∥BC;
(2)![]()
证明:如图2,设CE与BD交点为G,

![]() 是
是![]() 是外角,
是外角,
![]()
![]()
![]()
![]() 中,
中, ![]()
![]()
又![]()
![]()
(3)如图3,设![]() 则
则![]()

![]()
![]()
∵DF∥BC,
![]()
又![]()
![]()
![]()
![]()
又![]()
![]()
![]() 中,
中, ![]()

练习册系列答案
相关题目