题目内容
如图,已知,CE是Rt△ABC的斜边AB上的高,点P是CE的延长线上任意一点,BG⊥AP,


求证:(1)△AEP∽△DEB;
(2)CE2=ED·EP。若点P在线段CE上或EC的延长线上时(如图2和图3),上述结论CE2=ED?EP还成立吗?若成立,请给出证明;若不成立,请说明理由。(图2和图3挑选一张给予说明即可)
(2)CE2=ED·EP。若点P在线段CE上或EC的延长线上时(如图2和图3),上述结论CE2=ED?EP还成立吗?若成立,请给出证明;若不成立,请说明理由。(图2和图3挑选一张给予说明即可)
解:(1))CE是Rt△ABC的斜边AB上的高,BG⊥AP,
∴∠P+∠PAE=90°,∠DBE+∠PAE=90°,
∴∠P=∠DBE,
又∠AEP=∠DEB=90°,
∴△AEP∽△DEB。
(2)选择图2,成立
∵CE是Rt△ABC的斜边AB上的高,
∴△ACE∽△CBE
∴
即CE2=AE·BE。
和(1)中的证明同理,得△AEP∽△DEB
∴
即AE·BE=EP·ED
则△AEP∽△DEB
∴BE=
∵CE2=AE·BE
∴CE2=ED·EP。
∴∠P+∠PAE=90°,∠DBE+∠PAE=90°,
∴∠P=∠DBE,
又∠AEP=∠DEB=90°,
∴△AEP∽△DEB。
(2)选择图2,成立
∵CE是Rt△ABC的斜边AB上的高,
∴△ACE∽△CBE
∴

即CE2=AE·BE。
和(1)中的证明同理,得△AEP∽△DEB
∴

即AE·BE=EP·ED
则△AEP∽△DEB
∴BE=

∵CE2=AE·BE
∴CE2=ED·EP。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 如图,已知四边形ABCD是平行四边形,FC=5.4cm,CE=2.7cm,BE=3.2cm,求DC的长.
如图,已知四边形ABCD是平行四边形,FC=5.4cm,CE=2.7cm,BE=3.2cm,求DC的长. 如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.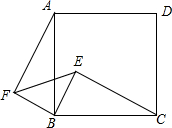 如图,已知四边形ABCD是正方形,E是正方形内一点,以BC为斜边作直角三角形BCE,又以BE为直角边作等腰直角三角形EBF,且∠EBF=90°,连接AF.
如图,已知四边形ABCD是正方形,E是正方形内一点,以BC为斜边作直角三角形BCE,又以BE为直角边作等腰直角三角形EBF,且∠EBF=90°,连接AF.