题目内容
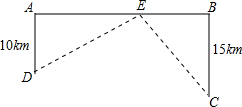（2012•金华模拟）如图，高速公路上有A、B两点相距25km，C、D为两村庄．已知DA=10km，CB=15km．DA⊥AB于A，CB⊥AB于B，现要在AB上建一个服务站E，使得C，D两村庄到E站的距离相等，则AE的长是15
15
km．分析：根据题意设出AE的长为x，再由勾股定理列出方程求解即可．
解答：解：设AE=x，则BE=25-x，
由勾股定理得：
在Rt△ADE中，
DE2=AD2+AE2=102+x2，
在Rt△BCE中，
CE2=BC2+BE2=152+（25-x）2，
由题意可知：DE=CE，
所以：102+x2=152+（25-x）2，
解得：x=15km．
所以，E应建在距A点15km处．
故答案为：15
由勾股定理得：
在Rt△ADE中，
DE2=AD2+AE2=102+x2，
在Rt△BCE中，
CE2=BC2+BE2=152+（25-x）2，
由题意可知：DE=CE，
所以：102+x2=152+（25-x）2，
解得：x=15km．
所以，E应建在距A点15km处．
故答案为：15
点评：本题考查正确运用勾股定理，善于观察题目的信息是解题以及学好数学的关键．
练习册系列答案
阅读快车系列答案
相关题目
（2012•金华模拟）如图，∠AOB=60°，点P在∠AOB的角平分线上，OP=10cm，点E、F是∠AOB两边OA，OB上的动点，当△PEF的周长最小时，点P到EF距离是（ ）
（2012•金华模拟）如图，在⊙O中，AB是直径，AD是弦，∠ADE=60°，∠C=30°．