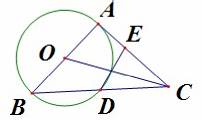
题目内容
如图以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E。
(1)求证:DE⊥AC;
(2)若∠ABC=30°,求tan∠BCO的值。
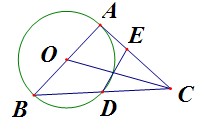
证明:(1)连接OD,∵DE是⊙o的 切线
∴DE⊥OD
∵O为BA中点,D为AC点 ∴AD=DC,A=OB, ∴OD∥AC
∴DE⊥AC
(2)过点O作OF⊥BD,则BF=FD
在Rt△ADB中, ∠B=30°
∴OF=1/2OB,BF= ![]() /2*OB
/2*OB
∵BD=DC,BF=FD ∴FC=3BF=3![]() /2*OB
/2*OB
在Rt△OFC中∴tan∠BOC=OF/FC=![]() /9
/9


练习册系列答案
相关题目
 交AC边于点E.
交AC边于点E.