题目内容
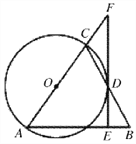
如图,在△ABC中,AB=AC,以AC为直径作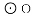
(1)求证: EF与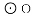
(2)若AE=6,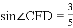 ,求EB的长.
,求EB的长.
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
题目内容
如图,在△ABC中,AB=AC,以AC为直径作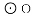
(1)求证: EF与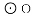
(2)若AE=6,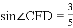 ,求EB的长.
,求EB的长.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案