题目内容
半径为2的⊙O中,弦AB⊥CD于E,且EO=1,则AB2+CD2的值为
- A.22
- B.24
- C.26
- D.28
D
分析:画出图形,过O作ON⊥AB于N,OM⊥CD于M,连接OA,OD,得出矩形ONEM,推出ON=EM,EN=OM,求出OM2+ON2=OE2=1,由垂径定理得出AN= AB,DM=
AB,DM= DC,由勾股定理求出4-
DC,由勾股定理求出4- DC2+4-
DC2+4- AB2=1,即可求出答案.
AB2=1,即可求出答案.
解答:
解:
过O作ON⊥AB于N,OM⊥CD于M,连接OA,OD,
∵AB⊥CD,
∴∠NEM=∠ENO=∠EMO=90°,
∴四边形NEMO是矩形,
∴ON=ME,OM=EN,
∵EN2+ON2=OE2=1,
∴OM2+ON2=OE2=1,
由垂径定理得:AN= AB,DM=
AB,DM= DC,
DC,
∵由勾股定理得:OM2=OD2-DM2=22-( )2,ON2=22-(
)2,ON2=22-( )2,
)2,
∴4- DC2+4-
DC2+4- AB2=1,
AB2=1,
即AB2+DC2=28,
故选D.
点评:本题考查了矩形的性质和判定,勾股定理,垂径定理等知识点,关键是构造直角三角形,能把已知条件和未知量联系起来.
分析:画出图形,过O作ON⊥AB于N,OM⊥CD于M,连接OA,OD,得出矩形ONEM,推出ON=EM,EN=OM,求出OM2+ON2=OE2=1,由垂径定理得出AN=
 AB,DM=
AB,DM= DC,由勾股定理求出4-
DC,由勾股定理求出4- DC2+4-
DC2+4- AB2=1,即可求出答案.
AB2=1,即可求出答案.解答:

解:
过O作ON⊥AB于N,OM⊥CD于M,连接OA,OD,
∵AB⊥CD,
∴∠NEM=∠ENO=∠EMO=90°,
∴四边形NEMO是矩形,
∴ON=ME,OM=EN,
∵EN2+ON2=OE2=1,
∴OM2+ON2=OE2=1,
由垂径定理得:AN=
 AB,DM=
AB,DM= DC,
DC,∵由勾股定理得:OM2=OD2-DM2=22-(
 )2,ON2=22-(
)2,ON2=22-( )2,
)2,∴4-
 DC2+4-
DC2+4- AB2=1,
AB2=1,即AB2+DC2=28,
故选D.
点评:本题考查了矩形的性质和判定,勾股定理,垂径定理等知识点,关键是构造直角三角形,能把已知条件和未知量联系起来.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
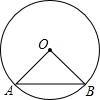 如图,在半径为2的⊙O中,弦AB的长为2
如图,在半径为2的⊙O中,弦AB的长为2 如图,半径为4的⊙O中有弦AB,以AB为折痕对折,劣弧恰好经过圆心O,则弦AB的长度为
如图,半径为4的⊙O中有弦AB,以AB为折痕对折,劣弧恰好经过圆心O,则弦AB的长度为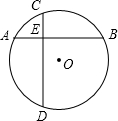 如图,在半径为6cm的⊙O中,弦AB⊥CD,垂足为E,若CE=3cm,DE=7cm,则AB=
如图,在半径为6cm的⊙O中,弦AB⊥CD,垂足为E,若CE=3cm,DE=7cm,则AB=