题目内容
如图，一个大正方形被两条线段分割成两个小正方形和两个长方形，如果S1=75cm2，S2=15cm2，那么大正方形的面积是S=________cm2．
108
分析：根据正方形面积计算公式，已知正方形面积可以求出正方形的边长，根据矩形面积计算公式求出最小小正方形的边长，计算面积，即可求解．
解答：
解：已知正方形BHOF面积为75cm2，∴OH=
=
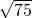cm，
矩形OHCG的面积为15cm2，∴OG=
=
cm，
∴正方形OEDG的面积为
cm2=3cm2，
故正方形ABCD的面积=（75+15+15+3）cm2=108cm2，
故答案为 108．
点评：本题考查了正方形、矩形面积的计算，计算正方形DEOG的边长并求面积是解题的关键．
分析：根据正方形面积计算公式，已知正方形面积可以求出正方形的边长，根据矩形面积计算公式求出最小小正方形的边长，计算面积，即可求解．
解答：
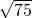解：已知正方形BHOF面积为75cm2，∴OH==cm，矩形OHCG的面积为15cm2，∴OG=
=cm，∴正方形OEDG的面积为
cm2=3cm2，故正方形ABCD的面积=（75+15+15+3）cm2=108cm2，
故答案为 108．
点评：本题考查了正方形、矩形面积的计算，计算正方形DEOG的边长并求面积是解题的关键．
练习册系列答案
相关题目
9、如图，一个大正方形被两条线段分割成两个小正方形和两个长方形，如果S1=64cm2，S2=16cm2，那么小正方形的面积是S3=
面积是S3=________cm2．