题目内容
19.先化简,再求值:$\frac{m-4}{{m}^{2}-9}$•(1+$\frac{14m-7}{{m}^{2}-8m+16}$)÷$\frac{1}{m-3}$,选择一个你喜欢且使原式有意义的m的值代入求值.分析 先根据分式混合运算的法则把原式进行化简,再选出合适的m的值代入进行计算即可.
解答 解:原式=$\frac{m-4}{(m+3)(m-3)}$•$\frac{(m+3)^{2}}{(m-4)^{2}}$•(m-3)
=$\frac{m+3}{m-4}$,
当m=2时,原式=$\frac{2+3}{2-4}$=-$\frac{5}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.下列多项式中不能用公式分解的是( )
| A. | -a2-b2+2ab | B. | a2+a+$\frac{1}{4}$ | C. | -a2+25b2 | D. | -4-b2 |
 如图,AB∥CD,AD=10,AO=7,CO=6,求BO的长.
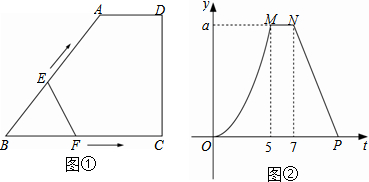
如图,AB∥CD,AD=10,AO=7,CO=6,求BO的长.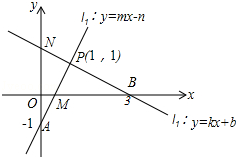 如图,请根据图象所提供的信息解答下列问题:
如图,请根据图象所提供的信息解答下列问题: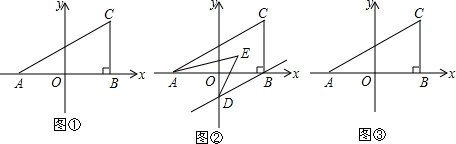
 画图:
画图: