题目内容
如图，已知BE平分∠ABC，DE∥BC，AD=3，DE=2，AC=4，则AE=考点：平行线分线段成比例,等腰三角形的判定与性质
专题：
分析：如图，首先证明BD=DE，求出AB=5；证明△ADE∽△ABC，列出比例式
=
，求出AE即可解决问题．
| AD |
| AB |
| AE |
| AC |
解答：解：如图，∵BE平分∠ABC，DE∥BC，
∴∠DBE=∠CBE，∠DEB=∠CBE，
∴∠DBE=∠DEB，
∴DB=DE=2，AB=AD+DB=5；
∵DE∥BC，
∴△ADE∽△ABC，
∴
=
，而AC=4，AD=3，
∴AE=2.4，
故答案为2.4．
解：如图，∵BE平分∠ABC，DE∥BC，∴∠DBE=∠CBE，∠DEB=∠CBE，
∴∠DBE=∠DEB，
∴DB=DE=2，AB=AD+DB=5；
∵DE∥BC，
∴△ADE∽△ABC，
∴
| AD |
| AB |
| AE |
| AC |
∴AE=2.4，
故答案为2.4．
点评：该题主要考查了等腰三角形的判定、相似三角形的判定及其性质等几何知识点及其应用问题；牢固掌握等腰三角形的判定、相似三角形的判定及其性质是解题的关键．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
在-
，-|12|，-20，0，-（-5）中，负数的个数有（ ）
| 1 |
| 2 |
| A、2个 |
| B、3 个 |
| C、4 个 |
| D、5 个 |
下列说法正确的是（ ）
| A、两名同学5次平均分相同，则方差较大的同学成绩更稳定 |
| B、一组数据3，4，4，6，8，5的众数为4 |
| C、必然事件的概率是100%，随机事件的概率是50% |
| D、了解全国每天丢弃的塑料袋的数量，应适合普查的方法 |
下列运算中，正确的是（ ）
| A、x3+x3=2x6 |
| B、（a+b）2=a2+b2 |
| C、（x2）3=x5 |
| D、x3•x3=x6 |
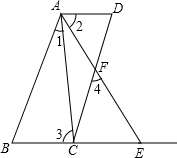如图AB∥CD．∠1=∠2，∠3=∠4，试说明AD∥BE．