题目内容
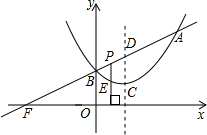
如图,已知二次函数y=-| 1 | 2 |
(1)求c的值;
(2)若△ABC的面积为3,求该二次函数的解析式;
(3)设D是(2)中所确定的二次函数图象的顶点,试问在直线AC上是否存在一点P,
 使△PBD的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
使△PBD的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)OA与OB的长,就是方程=-
x2+bx+c=0的两解,根据韦达定理就可以表示出OA•OB=-2c,OC的长是函数与y轴的交点的纵坐标的绝对值,因而OC2=c2.根据OC2=OA•OB就可以求出c的值.
(2)S△ABC=
AB•OC,根据韦达定理可以表示出AB的长,AB边上的高就是C点的纵坐标的绝对值,根据△ABC的面积为3就可以求出b的值,从而求出函数的解析式.
(3)根据二次函数的求根公式就可以求出二次函数的顶点D坐标.过B作BE⊥AC并延长BE到F使EF=BE,则点F和B关于直线AC对称,连接DF,交直线AC于点P,所作的点P满足△PBD的周长最小.可以求出直线AC与直线DF的交点.
| 1 |
| 2 |
(2)S△ABC=
| 1 |
| 2 |
(3)根据二次函数的求根公式就可以求出二次函数的顶点D坐标.过B作BE⊥AC并延长BE到F使EF=BE,则点F和B关于直线AC对称,连接DF,交直线AC于点P,所作的点P满足△PBD的周长最小.可以求出直线AC与直线DF的交点.
解答:解:(1)设A(x1,0),B(x2,0),
∵x2-2bx-2c=0,则x1+x2=2b,x1•x2=-2c
∵二次函数y=-
x2+bx+c的图象与y轴交于点C,
∴C(0,c),
由已知OC2=OA•OB得c2=x1•x2
∴c2=-2c,
又∵c<0,
∴c=-2.
(2)S△ABC=
AB•OC=
|x2-x1|•|-c|
=|x2-x1|=
=
当S△ABC=3时,
=3,得b2=
,
又∵该二次函数的对称轴在y轴的右侧,
∴b>0,
∴b=
,
∴该二次函数的解析式为y=-
x2+
x-2
(3)过B作BE⊥AC并延长BE到F使EF=BE,则点F和B关于直线AC对称,
连接DF,交直线AC于点P,则PB+PD=PF+PD=FD,
若直线AC上另外选一点P'',则P''B+P''D=P''F+P''D>FD,
∴PB+PD<P''B+P''D,
∴直线AC上的所有点中,存在P到点B和点D的距离和最小,而DB是定值,故所作的点P满足△PBD的周长最小.
作DH⊥x轴,垂足为H,作FG⊥x轴于G点,
由二次函数y=-
x2+
x-2
∴A(1,0),B(4,0),D(
,
)
∴OA=1,OB=4,OC=2,
∵∠BEA=∠AOC=90°,∠BAE=∠OAC,
∴△EAB∽△OAC,
∴
=
,
=
,而AB=3
∴AE=
,BE=
,
∴BF=
,
同理,由Rt△FGB∽Rt△AEB得,
=
,
=
,
∴FG=
,GB=
,
∴OH=
-4=
,
∴F(-
,
),
设过点D(
,
),F(-
,
)的直线的解析式为y=kx+n,则
,
解得
,
∴y=-
x+
,
而过点A(1,0)和C(0,-2)的直线的解析式为y=2x-2,
由
,
得
.
∴点P(
,
)为所求.
∵x2-2bx-2c=0,则x1+x2=2b,x1•x2=-2c
∵二次函数y=-
| 1 |
| 2 |
∴C(0,c),
由已知OC2=OA•OB得c2=x1•x2
∴c2=-2c,
又∵c<0,
∴c=-2.
(2)S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
=|x2-x1|=
| (x1+x2)2-4x1x2 |
| 4b2-16 |
当S△ABC=3时,
| 4b2-16 |
| 25 |
| 4 |
又∵该二次函数的对称轴在y轴的右侧,
∴b>0,
∴b=
| 5 |
| 2 |
∴该二次函数的解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
(3)过B作BE⊥AC并延长BE到F使EF=BE,则点F和B关于直线AC对称,
连接DF,交直线AC于点P,则PB+PD=PF+PD=FD,

若直线AC上另外选一点P'',则P''B+P''D=P''F+P''D>FD,
∴PB+PD<P''B+P''D,
∴直线AC上的所有点中,存在P到点B和点D的距离和最小,而DB是定值,故所作的点P满足△PBD的周长最小.
作DH⊥x轴,垂足为H,作FG⊥x轴于G点,
由二次函数y=-
| 1 |
| 2 |
| 5 |
| 2 |
∴A(1,0),B(4,0),D(
| 5 |
| 2 |
| 9 |
| 8 |
∴OA=1,OB=4,OC=2,
∵∠BEA=∠AOC=90°,∠BAE=∠OAC,
∴△EAB∽△OAC,
∴
| AE |
| AB |
| OA |
| AC |
| BE |
| AB |
| OC |
| AC |
∴AE=
3
| ||
| 5 |
6
| ||
| 5 |
∴BF=
12
| ||
| 5 |
同理,由Rt△FGB∽Rt△AEB得,
| FG |
| FB |
| AE |
| AB |
| BG |
| FB |
| BE |
| AB |
∴FG=
| 12 |
| 5 |
| 24 |
| 5 |
∴OH=
| 24 |
| 5 |
| 4 |
| 5 |
∴F(-
| 4 |
| 5 |
| 12 |
| 5 |
设过点D(
| 5 |
| 2 |
| 9 |
| 8 |
| 4 |
| 5 |
| 12 |
| 5 |
|
解得
|
∴y=-
| 17 |
| 44 |
| 23 |
| 11 |
而过点A(1,0)和C(0,-2)的直线的解析式为y=2x-2,
由
|
得
|
∴点P(
| 12 |
| 7 |
| 10 |
| 7 |
点评:本题主要考查了二次函数与一元二次方程的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
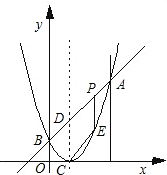 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.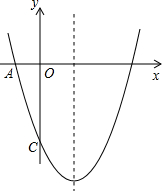 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).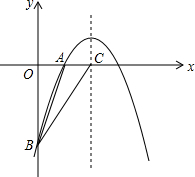 (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数