题目内容
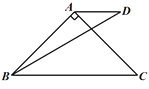
【题目】菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,连接EF.
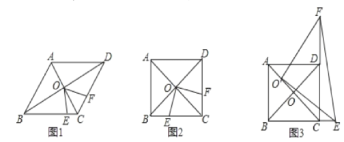
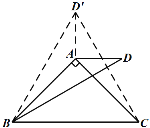
(1)如图2,当∠ABC=60°时,猜想三条线段CE、CF、AB之间的数量关系___;
(2)如图1,当∠ABC=90°时,若AC=4![]() ,BE=
,BE=![]() ,求线段EF的长;
,求线段EF的长;
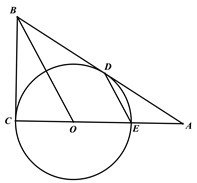
(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系,请直接写出你的结论.
【答案】(1)CE+CF=![]() AB;(2)
AB;(2)![]() ;(3)CFCE =
;(3)CFCE =![]() O`C.
O`C.
【解析】
(1)如图1中,连接EF,在CO上截取CN=CF,只要证明△OFN≌△EFC,即可推出CE+CF=OC,再证明OC=![]() AB即可.
AB即可.
(2)先证明△OBE≌△OCF得到BE=CF,在Rt△CEF中,根据CE![]() +CF
+CF![]() =EF
=EF![]() 即可解决问题.
即可解决问题.
(3)结论:CF-CE=![]() O`C,过点O`作O`H⊥AC交CF于H,只要证明△FO`H≌△EO
O`C,过点O`作O`H⊥AC交CF于H,只要证明△FO`H≌△EO![]() C,推出FH=CE,再根据等腰直角三角形性质即可解决问题.
C,推出FH=CE,再根据等腰直角三角形性质即可解决问题.
(1)结论CE+CF=![]() AB.
AB.
理由:如图1中,连接EF,在CO上截取CN=CF.

∵∠EOF+∠ECF=180°,
∴O、E. C. F四点共圆,
∵∠ABC=60°,四边形ABCD是菱形,
∴∠BCD=180°∠ABC=120°,
∴∠ACB=∠ACD=60°,
∴∠OEF=∠OCF,∠OFE=∠OCE,
∴∠OEF=∠OFE=60°,
∴△OEF是等边三角形,
∴OF=FE,
∵CN=CF,∠FCN=60°,
∴△CFN是等边三角形,
∴FN=FC,∠OFE=∠CFN,
∴∠OFN=∠EFC,
在△OFN和△EFC中,
 ,
,
∴△OFN≌△EFC,
∴ON=EC,
∴CE+CF=CN+ON=OC,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠CBO=30°,AC⊥BD,
在RT△BOC中,∵∠BOC=90°,∠OBC=30°,
∴OC=![]() BC=
BC=![]() AB,
AB,
∴CE+CF=![]() AB.
AB.
(2)连接EF

∵在菱形ABCD中
∴菱形ABCD是正方形,
∴∠BOC=90°,OB=OC,AB=AC,∠OBE=∠OCF=45°,∠BCD=90°
∵∠EOF+∠BCD=180°,
∴∠EOF=90°,
∴∠BOE=∠COF
∴△OBE≌△OCF,
∴BE=CF,
∵BE=![]() ,
,
∴CF=![]() ,
,
在Rt△ABC中,AB![]() +BC
+BC![]() =AC
=AC![]() ,AC=4
,AC=4![]()
∴BC=4,
∴CE=![]() ,
,
在Rt△CEF中,CE![]() +CF
+CF![]() =EF
=EF![]() ,
,
∴EF=![]()
答:线段EF的长为![]() ,
,
(3)结论:CFCE=![]() O`C.
O`C.
理由:过点O`作O`H⊥AC交CF于H,

∵∠O`CH=∠O`HC=45°,
∴O`H=O`C,
∵∠FO`E=∠HO`C,
∴∠FO`H=∠CO`E,
∵∠EO`F=∠ECF=90°,
∴O`.C. F. E四点共圆,
∴∠O`EF=∠OCF=45°,
∴∠O`FE=∠O`EF=45°,
∴O`E=O`F,
在△FO`H和△EO`C中,
 ,
,
∴△FO`H≌△EO![]() C,
C,
∴FH=CE,
∴CFCE=CFFH=CH=![]() O`C.
O`C.

 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案【题目】A、B两校举行初中数学联赛,各校从九年级学生中挑选50人参加,成绩统计如下表:
成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | A | 2 | 5 | 10 | 13 | 14 | 6 |
B | 4 | 4 | 16 | 2 | 12 | 12 | |
请你根据所学知识和表中数据,判断这两校学生在这次联赛中的成绩谁优谁次?