��Ŀ����
����Ŀ����1���Ķ�������ϣ�
��![]() ��
��![]() �������Ϸֱ��ʾʵ��
�������Ϸֱ��ʾʵ��![]() ��
��![]() ��
��![]() ��
��![]() ����֮��ľ�߱�ʾΪ
����֮��ľ�߱�ʾΪ![]()
��![]() ��
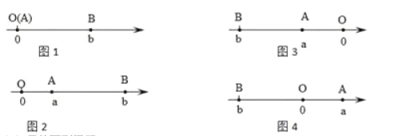
��![]() ��������һ����ԭ��ʱ���������
��������һ����ԭ��ʱ���������![]() ��ԭ�㣬��ͼ1��
��ԭ�㣬��ͼ1��![]() ��
��
��![]() ��
��![]() ������ԭ��ʱ��
������ԭ��ʱ��
����ͼ2����![]() ��
��![]() ����ԭ����Ҳ࣬
����ԭ����Ҳ࣬![]() ��
��
����ͼ3����![]() ��
��![]() ����ԭ�����࣬
����ԭ�����࣬![]() ��
��
����ͼ4����![]() ��
��![]() ��ԭ������࣬
��ԭ������࣬![]() ��
��
��2���ش��������⣺
�������ϱ�ʾ2��5�������ľ����� �������ϱ�ʾ-2��-5������֮��ľ����� �������ϱ�ʾ1��-3������֮��ľ����� ��
�������ϱ�ʾ![]() ��-1������
��-1������![]() ��
��![]() ֮��ľ����� �����
֮��ľ����� �����![]() ����ô
����ô![]() Ϊ ��
Ϊ ��
��������ʽ![]() ȡ��Сֵʱ����Ӧ��
ȡ��Сֵʱ����Ӧ��![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
����![]() ����Сֵ����ʾ��
����Сֵ����ʾ��![]() .
.
���𰸡���3,3,4����![]() ��1��
��1��![]() ����
����![]() ����
����![]() .
.
��������
�����ݣ�1���е��������빫ʽ����𰸣�
�����ݣ�1���е��������빫ʽ�г�������⣻
�������߶��ϵĵ㵽���˵ľ���֮����С�ɵý����
�������߶��ϵĵ㵽���˵ľ���֮����С�г���ʽ���㼴�ɣ�
�⣺����ʾ2��5�������ľ���Ϊ![]() ��
��
��ʾ-2��-5������֮��ľ���Ϊ![]() ��
��
��ʾ1��-3������֮��ľ���Ϊ![]() ��
��
����ʾ![]() ��-1������
��-1������![]() ��
��![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ��
��
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]()
��![]() ����
����![]() ��
��![]() �ľ��룬
�ľ��룬![]() ��ʾ
��ʾ![]() ��
��![]() �ľ��룬��
�ľ��룬��![]() ��
��![]() ��2֮��ʱ������֮����С����
��2֮��ʱ������֮����С����![]() ȡ��Сֵʱ����Ӧ��
ȡ��Сֵʱ����Ӧ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]()
��������֪��Ҫʹ![]() ��С����
��С����![]() ��1��2015֮�伴�ɣ�
��1��2015֮�伴�ɣ�
Ҫʹ![]() ��С����
��С����![]() ��2��2014֮�伴�ɡ���
��2��2014֮�伴�ɡ���
�Դ����ƣ�Ҫʹ![]() ��С����
��С����![]() ��1007��1009֮�伴�ɣ�
��1007��1009֮�伴�ɣ�
���ʣ��![]() ��Сʱ��ȡ
��Сʱ��ȡ![]() ���ɣ���
���ɣ���![]() ʱ��
ʱ��
ԭʽ![]()
![]()
![]()
![]()