题目内容

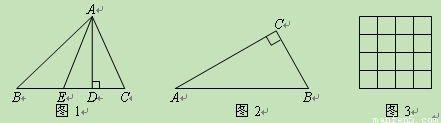
如图1，AD和AE分别是△ABC的BC边上的高和中线，点D是垂足，点E是BC的中点，规定：λA=
DE
BD
．如图2，在△ABC中，∠C=90°，∠A=30°，λC=
1
3
1
3
．
分析：设CB的长为a，然后分别利用解直角三角形求得DE与EA的长，然后求值即可．
解答：解：如图：CD⊥AB，E为AB的中点，
∴BE=BC=EA=a
设CB=a，
∵∠C=90°，∠A=30°，
∴∠ECD=∠BCD=30°，
∴BD=ED=
a
2
，
∴λC=
DE
DA
=
a
2
3a
2
=
1
3
，
故答案为
1
3
．
点评：本题考查了直角三角形及三角形的角平分线、中线和高的知识，属于基础题，比较简单．
练习册系列答案
相关题目
如图1，AD和AE分别是△ABC的BC边上的高和中线，点D是垂足，点E是BC的中点，规定：λA=
DEBE
．特别地，当点D、E重合时，规定：λA=0．另外，对λB、λC作类似的规定．
精英家教网
（1）如图2，在△ABC中，∠C=90°，∠A=30°，求λA、λC；
（2）在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点（格点即每个小正方形的顶点）上，且λA=2，面积也为2；
（3）判断下列三个命题的真假（真命题打“√”，假命题打“×”）：
①若△ABC中λA＜1，则△ABC为锐角三角形；
 

②若△ABC中λA=1，则△ABC为直角三角形；
 

③若△ABC中λA＞1，则△ABC为钝角三角形．
 
．
操作探究：
我们知道一个三角形中有三条高线和三条中线．如图1，AD和AE分别是△ABC中BC边上的高线和中线，我们规定：kA=
DE
BE′
，另外，对kB、kC作类似的规定．
（1）如图2，在△ABC中，∠C=90°，∠A=30°，则kA的值为
1
1
，kC的值为
1
2
1
2
；
（2）在每个小正方形边长均为1的4×4的方格纸上（如图3），画一个△ABC，使其顶点在格点（格点即每个小正方形的顶点）上，且kA=2，面积也为2；
（3）判断下面三个命题的真假（真命题打“√”，假命题的打“×”）
①若△ABC中，kA＜1，则△ABC为锐角三角形
×
×
；
②若△ABC中，kA=1，则△ABC为直角三角形
√
√
；
③若△ABC中，kA＞1，则△ABC为钝角三角形
√
√
．
（11·台州）(12分)如图1，AD和AE分别是△ABC的BC边上的高和中线，
点D是垂足，点E是BC的中点，规定：．特别地，当点D、E重合时，规定：λA
＝0．另外，对λB、λC作类似的规定．

(1)如图2，在△ABC中，∠C＝90º，∠A＝30º，求λA、λC；
(2)在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点(格点即每个小正方形的顶点)上，且λA＝2，面积也为2；
(3)判断下列三个命题的真假(真命题打“P”，假命题打“×”)：
①若△ABC中λA＜1，则△ABC为锐角三角形；【   】
②若△ABC中λA＝1，则△ABC为锐角三角形；【   】
③若△ABC中λA＞1，则△ABC为锐角三角形．【   】

（11·台州）(12分)如图1，AD和AE分别是△ABC的BC边上的高和中线，

点D是垂足，点E是BC的中点，规定：．特别地，当点D、E重合时，规定：λA

＝0．另外，对λB、λC作类似的规定．

(1)如图2，在△ABC中，∠C＝90º，∠A＝30º，求λA、λC；

(2)在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点(格点即每个小正方形的顶点)上，且λA＝2，面积也为2；

(3)判断下列三个命题的真假(真命题打“P”，假命题打“×”)：

①若△ABC中λA＜1，则△ABC为锐角三角形；【    】

②若△ABC中λA＝1，则△ABC为锐角三角形；【    】

③若△ABC中λA＞1，则△ABC为锐角三角形．【    】

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网