题目内容
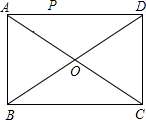 如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )
如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
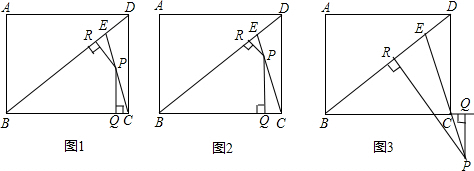
分析:过P点作PE⊥AC,PF⊥BD,由矩形的性质可证△PEA∽△CDA和△PFD∽△BAD,根据
=
和
=
,即
=
和
=
,两式相加得PE+PF=
,即为点P到矩形的两条对角线AC和BD的距离之和.
| PE |
| CD |
| PA |
| CA |
| PF |
| AB |
| PD |
| BD |
| PE |
| 3 |
| PA |
| 5 |
| PF |
| 3 |
| PD |
| 5 |
| 12 |
| 5 |
解答:解:法1:过P点作PE⊥AC,PF⊥BD
∵矩形ABCD
∴AD⊥CD
∴△PEA∽△CDA
∴
=
∵AC=BD=
=5
∴
=
…①
同理:△PFD∽△BAD
∴
=
∴
=
…②
∴①+②得:
=
=
=
∴PE+PF=
即点P到矩形的两条对角线AC和BD的距离之和是
.
法2: 连结OP.
连结OP.
∵AD=4,CD=3,
∴AC=
=5,
又∵矩形的对角线相等且互相平分,
∴AO=OD=2.5cm,
∴S△APO+S△POD=
×2.5•PE+
×2.5•PF=
×2.5(PE+PF)=
×3×4,
∴PE+PF=
.
∵矩形ABCD

∴AD⊥CD
∴△PEA∽△CDA
∴
| PE |
| CD |
| PA |
| CA |
∵AC=BD=
| 32+42 |
∴
| PE |
| 3 |
| PA |
| 5 |
同理:△PFD∽△BAD
∴
| PF |
| AB |
| PD |
| BD |
∴
| PF |
| 3 |
| PD |
| 5 |
∴①+②得:
| PE+PF |
| 3 |
| PA+PD |
| 5 |
| AD |
| 5 |
| 4 |
| 5 |
∴PE+PF=
| 12 |
| 5 |
即点P到矩形的两条对角线AC和BD的距离之和是
| 12 |
| 5 |
法2:
 连结OP.
连结OP.∵AD=4,CD=3,
∴AC=
| 32+42 |
又∵矩形的对角线相等且互相平分,
∴AO=OD=2.5cm,
∴S△APO+S△POD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴PE+PF=
| 12 |
| 5 |
点评:根据矩形的性质,结合相似三角形求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 12、如图,点E是矩形ABCD中BC边的中点,AB=6,当AE⊥DE时,矩形ABCD的周长是( )
12、如图,点E是矩形ABCD中BC边的中点,AB=6,当AE⊥DE时,矩形ABCD的周长是( ) 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合.若BC=3,则折痕CE的长为
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合.若BC=3,则折痕CE的长为 (2013•宝应县一模)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,求折痕CE的长.
(2013•宝应县一模)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,求折痕CE的长. 如图,点P是矩形ABCD对角线BD上的一个动点,AB=6,AD=8,则PA+PC的最小值为
如图,点P是矩形ABCD对角线BD上的一个动点,AB=6,AD=8,则PA+PC的最小值为