题目内容
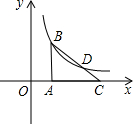 如图,直线y=
如图,直线y=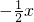 +3与双曲线y=
+3与双曲线y= (x>0)相交于B,D两点,交x轴于C点,若点D是BC的中点,则k=
(x>0)相交于B,D两点,交x轴于C点,若点D是BC的中点,则k=
- A.1
- B.2
- C.3
- D.4
D
分析:首先根据直线y=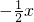 +3可以求出 C的坐标,然后设B(x1,y1),D(x2,y2),由D是BC中点得到 2x2=x1+6 ①,
+3可以求出 C的坐标,然后设B(x1,y1),D(x2,y2),由D是BC中点得到 2x2=x1+6 ①,
联立方程y=- x+3,y=
x+3,y= ,然后消去y得
,然后消去y得 x2-3x+k=0,接着利用韦达定理可以得到 x1+x2=6②,x1x2=2k③,联立它们即可求解.
x2-3x+k=0,接着利用韦达定理可以得到 x1+x2=6②,x1x2=2k③,联立它们即可求解.
解答:∵直线y=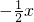 +3,
+3,
∴当y=0时,x=6,
∴C(6,0),
设B(x1,y1),D(x2,y2),
∵D是BC中点,
那么 2x2=x1+6,
∴x1=2x2-6①,
联立方程y=- x+3,y=
x+3,y= ,然后消去y得
,然后消去y得
- x+3=
x+3= ,
,
∴ x2-3x+k=0,
x2-3x+k=0,
根据韦达定理
x1+x2=6②,
x1x2=2k③,
用①代入②3x2-6=6,
∴x2=4,
∴x1=2×4-6=2,
由③2k=x1x2=8,
那么k=4.
故选D.
点评:此题主要考查了一次函数与反比例函数的交点坐标问题,同时也利用了中点坐标的公式,其中利用方程组和待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.
分析:首先根据直线y=
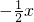 +3可以求出 C的坐标,然后设B(x1,y1),D(x2,y2),由D是BC中点得到 2x2=x1+6 ①,
+3可以求出 C的坐标,然后设B(x1,y1),D(x2,y2),由D是BC中点得到 2x2=x1+6 ①,联立方程y=-
 x+3,y=
x+3,y= ,然后消去y得
,然后消去y得 x2-3x+k=0,接着利用韦达定理可以得到 x1+x2=6②,x1x2=2k③,联立它们即可求解.
x2-3x+k=0,接着利用韦达定理可以得到 x1+x2=6②,x1x2=2k③,联立它们即可求解.解答:∵直线y=
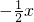 +3,
+3,∴当y=0时,x=6,
∴C(6,0),
设B(x1,y1),D(x2,y2),
∵D是BC中点,
那么 2x2=x1+6,
∴x1=2x2-6①,
联立方程y=-
 x+3,y=
x+3,y= ,然后消去y得
,然后消去y得-
 x+3=
x+3= ,
,∴
 x2-3x+k=0,
x2-3x+k=0,根据韦达定理
x1+x2=6②,
x1x2=2k③,
用①代入②3x2-6=6,
∴x2=4,
∴x1=2×4-6=2,
由③2k=x1x2=8,
那么k=4.
故选D.
点评:此题主要考查了一次函数与反比例函数的交点坐标问题,同时也利用了中点坐标的公式,其中利用方程组和待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线y=k1x与双曲线y=
如图,直线y=k1x与双曲线y= 如图,直线y=x与反比例函数y=
如图,直线y=x与反比例函数y= (2013•张家界)如图,直线x=2与反比例函数
(2013•张家界)如图,直线x=2与反比例函数 (2013•锦州)如图,直线y=mx与双曲线y=
(2013•锦州)如图,直线y=mx与双曲线y= 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=