题目内容
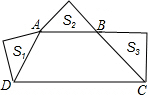
梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是S1、S2、S3,且S1+S3=9S2,则CD=( )
A.2.5AB
B.3AB
C.3.5AB
D.4AB
【答案】分析:根据等腰直角三角形的面积公式,和勾股定理进行转换得出S1= ,S2,=
,S2,= ,S3=
,S3= ,结合已知条件推出AD2+BC2=9AB2,因为AD2+BC2=(DC-AB)2,所以代入化简得:CD=4AB,CD=-2AB(不符合题意,舍去),即可答案选D.
,结合已知条件推出AD2+BC2=9AB2,因为AD2+BC2=(DC-AB)2,所以代入化简得:CD=4AB,CD=-2AB(不符合题意,舍去),即可答案选D.
解答: 解:如图,作AO∥BC交DC于O点,AB∥CD,∠ADC+∠BCD=90°,
解:如图,作AO∥BC交DC于O点,AB∥CD,∠ADC+∠BCD=90°,
∴AB=OC,AO=BC,∠DAO=90°,
∵以AD、AB、BC为斜边向形外作等腰直角三角形,
∴S1= AM×MD=
AM×MD= AM2,
AM2,
根据勾股定理得:AM2+MD2=AD2,
∵AM=MD,
∴2AM2=AD2,
∴S1= ,
,
同理:∵S2=AN2• ,2AN2=AB2,∴S2=
,2AN2=AB2,∴S2= ,
,
同理:∵S3=BP2• ,2BP2=BC2,∴S3=
,2BP2=BC2,∴S3= ,
,
∵S1+S3=9S2
∴ ,
,
∴(DC-AB)2=9AB2
∴(DO-3AB)(DO+3AB)=0,
∴DO=3AB,DO=-2AB(不合题意,舍去),
∴CD=DO+OC=3AB+AB=4AB.
故选D.
点评:本题主要考查勾股定理、三角形面积公式、梯形的性质、勾股定理、平行四边形的性质等知识点,本题的关键在于等量之间的转换.
 ,S2,=
,S2,= ,S3=
,S3= ,结合已知条件推出AD2+BC2=9AB2,因为AD2+BC2=(DC-AB)2,所以代入化简得:CD=4AB,CD=-2AB(不符合题意,舍去),即可答案选D.
,结合已知条件推出AD2+BC2=9AB2,因为AD2+BC2=(DC-AB)2,所以代入化简得:CD=4AB,CD=-2AB(不符合题意,舍去),即可答案选D.解答:
 解:如图,作AO∥BC交DC于O点,AB∥CD,∠ADC+∠BCD=90°,
解:如图,作AO∥BC交DC于O点,AB∥CD,∠ADC+∠BCD=90°,∴AB=OC,AO=BC,∠DAO=90°,
∵以AD、AB、BC为斜边向形外作等腰直角三角形,
∴S1=
 AM×MD=
AM×MD= AM2,
AM2,根据勾股定理得:AM2+MD2=AD2,
∵AM=MD,
∴2AM2=AD2,
∴S1=
 ,
,同理:∵S2=AN2•
 ,2AN2=AB2,∴S2=
,2AN2=AB2,∴S2= ,
,同理:∵S3=BP2•
 ,2BP2=BC2,∴S3=
,2BP2=BC2,∴S3= ,
,∵S1+S3=9S2
∴
 ,
,∴(DC-AB)2=9AB2
∴(DO-3AB)(DO+3AB)=0,
∴DO=3AB,DO=-2AB(不合题意,舍去),
∴CD=DO+OC=3AB+AB=4AB.
故选D.
点评:本题主要考查勾股定理、三角形面积公式、梯形的性质、勾股定理、平行四边形的性质等知识点,本题的关键在于等量之间的转换.

练习册系列答案
相关题目
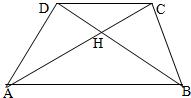 27、梯形ABCD中AB∥CD,对角线AC、BD垂直相交于H,M是AD上的点,MH所在直线交BC于N.在以上前提下,试将下列设定中的两个作为题设,另一个作为结论组成一个正确的命题,并证明这个命题.①AD=BC;②MN⊥BC;③AM=DM.
27、梯形ABCD中AB∥CD,对角线AC、BD垂直相交于H,M是AD上的点,MH所在直线交BC于N.在以上前提下,试将下列设定中的两个作为题设,另一个作为结论组成一个正确的命题,并证明这个命题.①AD=BC;②MN⊥BC;③AM=DM. 如图,直角梯形ABCD中AB∥CD,AB⊥AD,AB=3CD,反比例函数
如图,直角梯形ABCD中AB∥CD,AB⊥AD,AB=3CD,反比例函数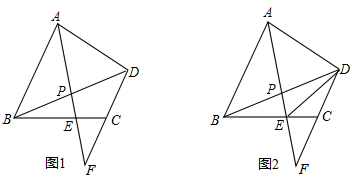
 如图,梯形ABCD中AB=CD、AC=3,则BD=
如图,梯形ABCD中AB=CD、AC=3,则BD=