题目内容
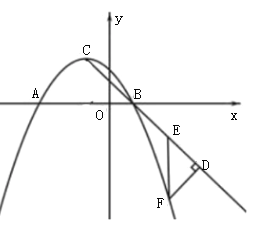
【题目】如图,△ABC中,BC=AC,∠ACB=90°,将△ABC绕着点C顺时针旋转α°(0≤α≤90°),得到△EFC,EF与AB、AC相交于点D、H,FC与AB相交于点G、AC相交于点D、H,FC与AB相较于点G.
(1)求证:△GBC≌△HEC;
(2)在旋转过程中,四边形BCED可以是某种特殊的平行四边形?并说明理由.
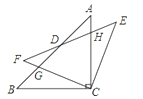
【答案】(1)详见解析;(2)当α=45°时,四边形BCED为菱形,理由详见解析.
【解析】
(1)先判断△ABC为等腰直角三角形得到∠A=∠B=45°,再根据旋转的性质得∠BCF=∠ACE=α,∠E=∠A=45°,CA=CE=CB,于是可根据“ASA”判断△GBC≌△HEC;
(2)当α=45°时,如图,根据旋转的性质得∠BCF=∠ACE=45°,则可计算出∠BCE=∠BCA+∠ACE=135°,所以∠B+∠BCE=180°,∠E+∠BCE=180°,所以BD∥CE,BC∥DE,于是可判断四边形BCED为平行四边形,加上CB=CE,则可判断四边形BCED为菱形.
(1)证明:∵BC=AC,∠ACB=90°,
∴△ABC为等腰直角三角形,
∴∠A=∠B=45°,
∵△ABC绕着点C顺时针旋转α°(0≤α≤90°),得到△EFC,
∴∠BCF=∠ACE=α,∠E=∠A=45°,CA=CE=CB,
在△GBC和△HEC中
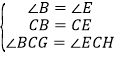 ,
,
∴△GBC≌△HEC;
(2)解:当α=45°时,四边形BCED为菱形.理由如下:
如图,∵∠BCF=∠ACE=45°,
∴∠BCE=∠BCA+∠ACE=90°+45°=135°,
而∠E=∠B=45°,
∴∠B+∠BCE=180°,∠E+∠BCE=180°,
∴BD∥CE,BC∥DE,
∴四边形BCED为平行四边形,
∵CB=CE,
∴四边形BCED为菱形.

【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.
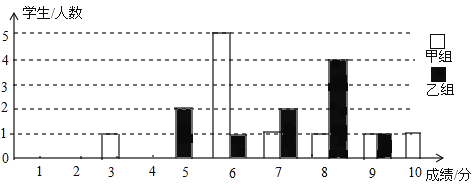
(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.