函数y=$\frac{1}{2x+1}$中.自变量x的取值范围是x≠-$\frac{1}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

2．函数y=$\frac{1}{2x+1}$中，自变量x的取值范围是x≠-$\frac{1}{2}$．

分析根据分式有意义的条件，分母不等于0，可以求出x的范围．

解答解：由题意得，2x+1≠0，
解得x≠-$\frac{1}{2}$．
故答案为x≠-$\frac{1}{2}$．

点评本题考查了函数自变量的取值范围问题，函数自变量的范围一般从三个方面考虑：
（1）当函数表达式是整式时，自变量可取全体实数；
（2）当函数表达式是分式时，考虑分式的分母不能为0；
（3）当函数表达式是二次根式时，被开方数非负．

练习册系列答案

13．小明在解关于x的方程$\frac{1+ax}{4}$=1-$\frac{1+x}{6}$，去分母乘12时常数1漏乘了，从而解出x=1，请你试着求出a的值，并求出方程正确的解．

10．若x=a-1是方程2x-3a=7的解，则a=-9．

17．现要估计鱼塘中鱼的数量，老李第一次捞出了180条，并做了记号，全部放回鱼塘，过几天又捞了一次，共200条，其中有3条带记号，你能帮老李估计出鱼塘里大约有多少条鱼吗？

7．为确保信息安全，信息需加密传输，发送方将明文加密为密文传输给接收方，接收方收到密文后解密还原为明文．已知某种加密规则为：明文a、b对应的密文为2a-1，3b-2．例如，明文1，2对应的密文是1，4，当接收方收收到密文是3，7时．解密得到的明文是（　　）

14．点A（10，0），B（6，3），点Q是x轴上一个动点．
（1）当△ABQ是直角三角形时，直接写出所有点Q的坐标；
（2）当△ABQ是等腰三角形时，请求出所有的点Q的坐标．

8．

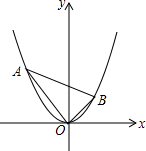如图，点A（a，b）是抛物线y=$\frac{1}{2}$x²上位于第二象限的一动点，OB⊥OA交抛物线于点B（c，d）．当点A在抛物线上运动的过程中，以下结论：①ac为定值；②ac=-bd；③△AOB的面积为定值；④直线AB必过一定点．其中正确的结论有（　　）

9．下列条件中一定能使△ABC≌△DEF成立的是（　　）

试题分类