Question

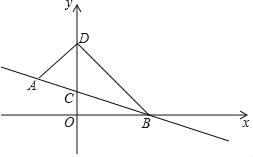
【题目】如图，在平面直角坐标系中，直线AB过点A(﹣1，1)，B(2，0)，交y轴于点C，点D (0，n)在点C上方．连接AD，BD．

(1)求直线AB的关系式；

(2)求△ABD的面积；(用含n的代数式表示)

(3)当S△ABD＝2时，作等腰直角三角形DBP，使DB＝DP，求出点P的坐标．

Answer 1

【答案】(1)y＝﹣x+；(2)n﹣1；(3)P(2，4)或(﹣2，0)．

【解析】

（1）设直线AB的解析式为：y＝kx+b，把点A（﹣1，1），B（2，0）代入即可得到结论；

（2）由（1）知：C（0，），得到CD＝n﹣，根据三角形的面积公式即可得到结论；

（3）根据三角形的面积得到D（0，2），求得OD＝OB，推出△BOD三等腰直角三角形，根据勾股定理得到BD＝2，根据等腰直角三角形的性质即可得到结论．

解：(1)设直线AB的解析式为：y＝kx+b，

把点A(﹣1，1)，B(2，0)代入得，，

解得：，

∴直线AB的关系式为：y＝﹣x+；

(2)由(1)知：C(0，)，

∴CD＝n﹣，

∴△ABD的面积＝×(n﹣)×1+(n﹣)×2＝n﹣1；

(3)∵△ABD的面积＝n﹣1＝2，

∴n＝2，

∴D(0，2)，

∴OD＝OB，

∴△BOD三等腰直角三角形，

∴BD＝2，

如图，∵△DBP是等腰直角三角形，DB＝DP，

∴∠DBP＝45°，

∴∠OBD＝45°，

∴∠OBP＝90°，

∴PB＝DB＝4，

∴P(2，4)或(﹣2，0)．

故答案为：(1)y＝﹣x+；(2)n﹣1；(3)P(2，4)或(﹣2，0)．