��Ŀ����
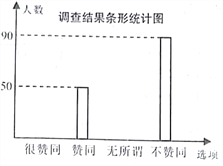
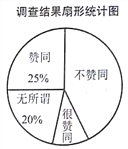
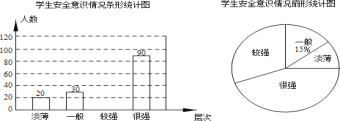
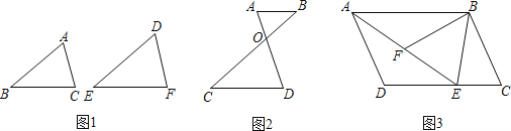
����Ŀ��Ϊ���˽�ij�о��꼶ѧ���������ɼ�(�ɼ���Ϊ����)�������ȡ�˲���ѧ���������ɼ����ֶ�(A��20.5��22.5��B��22.5��24.5��C��24.5��26.5��D��26.5��28.5��E��28.5��30.5)ͳ�����£������Ƴ�����ͼ��ʾ�IJ�������ͳ��ͼ��
�����ɼ�ͳ�Ʊ�
������ | Ƶ�� | Ƶ�� |
A | 12 | 0.05 |
B | 36 | a |
C | 84 | 0.35 |
D | b | 0.25 |
E | 48 | 0.20 |
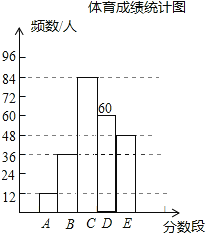
�����ɼ�ͳ��ͼ

���������ṩ����Ϣ������������⣺
(1)��ͳ�Ʊ��У�a��________��b��________������ͳ��ͼ����������
(2)С��˵�����������ݵ�����һ����C�У�������ΪС����˵����ȷ��__________(������ȷ������������)��
(3)���ɼ���27������(��27��)��Ϊ���㣬����н���48 000�����꼶ѧ���������ɼ�Ϊ�����ѧ��Լ�ж��٣�
���𰸡�(1) 0.15�� 60��(2) ��������3��21 600.
��������
��1������A����12�ˣ���Ӧ��Ƶ����0.05���������������Ȼ����ݰٷֱȵ��������a��b��ֵ��������ȫֱ��ͼ��
��2�����������Ķ��壬�Լ�ÿ���а���������ֻ���������������жϣ�
��3������������48000���Զ�Ӧ��Ƶ�ʼ�����⣮
��1���������������c=12��0.05=240���ˣ���
��a=![]() =0.15��b=240��0.25=60��
=0.15��b=240��0.25=60��
 ��
��
��2��C�����ݷ�Χ��24.5��26.5�����ڳɼ���Ϊ����������C��ijɼ�Ϊ25��26����ȻC��������࣬����25��26��������һ����࣮
�ʴ��ǣ�����
��3��48000����0.25+0.20��=21600���ˣ���
������48000�����꼶ѧ���������ɼ�Ϊ�����ѧ������Լ��21600�ˣ�

 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д�����Ŀ��ij�˶�Ь�������������ijУ40��Ů�����˶�Ь���룬������±���
Ь�ĺ��� | 35.5 | 36 | 36.5 | 37 | 37.5 |
���� | 4 | 6 | 16 | 12 | 2 |
���ڸþ�����Ҫ��200˫��������Ů�˶�Ь������ΪӦ�����������ȽϺ�����