题目内容
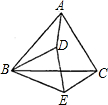如图，已知| AB |
| BD |
| BC |
| BE |
| CA |
| ED |
分析：由
=
=
，可得△ABC∽△DBE，从而得出∠ABC=∠DBE，即可得出∠ABD=∠EBC．
| AB |
| BD |
| BC |
| BE |
| CA |
| ED |
解答：证明：∵
=
=
，
∴△ABC∽△DBE（三边对应相等的两个三角形相似），
∴∠ABC=∠DBE，
∴∠ABC-∠DBC=∠DBE-∠DBC（等式的基本性质），
∴∠ABD=∠EBC．
| AB |
| BD |
| BC |
| BE |
| CA |
| ED |
∴△ABC∽△DBE（三边对应相等的两个三角形相似），
∴∠ABC=∠DBE，
∴∠ABC-∠DBC=∠DBE-∠DBC（等式的基本性质），
∴∠ABD=∠EBC．
点评：本题考查了相似三角形的判定和性质，主要考查了三边对应相等的两个三角形相似这个知识点．
练习册系列答案
阅读快车系列答案
相关题目
已知如图：
BD，ED
的最小值。
BD，ED
的最小值。